Изгиб прямого бруса

Рис. 14.6.

Рис. 14.5.

Рис. 14.4.

Изгибающий момент в поперечном сечении балки численно равен алгебраи­ческой сумме моментов (вычисленных относи­тельно центра тяжести сечения) внешних сил, действующих по одну сторону от данного сечения.

SМI = 0; Vа×z – Р×(z – x) – M = 0; откуда М = Vа×z – Р×(z – x).

Рис. 14.3.

Рис. 14.2.

Подвижные опоры дают возможность балке беспрепятствен­но изменять свою длину при изменении температуры и тем самым устраняют возможность появления температур­ных на­пряжений.

2. Неподвижная шарнирная опора (рис. 14.2, б). Такая опора допускает вращение конца балки, но устраняет поступа­тельное перемещение ее в любом направле­нии. Возникающую в ней реакцию можно разложить на две составляющие – гори­зон­тальную и вертикальную.

3. Жесткая заделка, или защемление (рис. 14.2, в). Такое закрепление не допус­кает ни линейных, ни угловых перемещений опорного сечения. В этой опоре может в об­щем случае возникать реакция, которую обычно раскладывают на две составляющие (вер­тикальную и горизонтальную) и момент защемления (ре­активный момент).

Балка с одним заделанным концом называется консольной балкой или просто кон­солью.

Если опорные реакции могут быть найдены из одних уравне­ний статики, то балки называют статически определимыми. Если же число неизвестных опорных реакций больше, чем число уравнений статики, возможных для данной задачи, то балки называют статически неопределимыми. Для определения реак­ций в таких балках приходится со­ставлять дополнительные уравнения – уравнения перемещений.

Определение внутренних усилий при изгибе

При плоском поперечном изгибе в поперечных сечениях балки возникают два внут­ренних усилия (внутренних силовых фактора) – изгибающий момент М и поперечная сила Q, Для их опреде­ления применим метод сечений. В интересующем нас месте сделаем мысленный разрез балки, напри­мер на расстоянии z от левой опо­ры (рис. 14.3, а). Отбро­сим одну из частей балки, например правую, и рассмотрим равновесие левой части.

Взаимодействие частей балки заменим внутренними усилиями: изгибающим момен­том М и по­перечной силой Q (рис. 14.3, б).

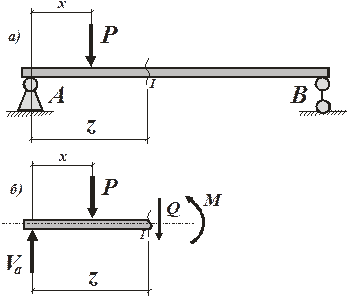
Для определения М и Q исполь­зуем два уравнения равновесия:

SУ = 0; V_а – Р – Q = 0; откуда Q = V_а – P;

Таким образом,

1) поперечная сила Q в поперечном сечении балки численно равна алгебраиче­ской сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от сечения;

Правило знаков для изгибающих моментов и поперечных сил

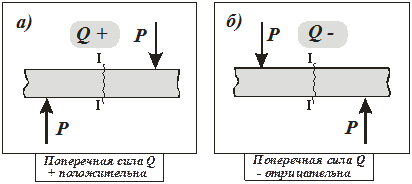
Поперечная сила в сечении балки I – I(рис. 14.4, а) считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа – сверху вниз, и отрицательной – в противоположном случае (рис. 14.4, б).

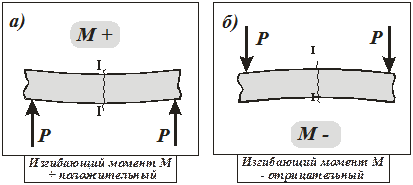
Изгибающий момент в сечении балки, например в сечении I – I(рис. 14.5 и 14.6, а), считается положительным, если равнодей­ствующий момент внешних сил слева от сечения направлен по часовой стрелке, а справа – против часовой стрелки, и отрица­тельным – в про­тивоположном случае (рис. 14.5 и 14.6, б). Моменты, изображенные на рисунках (а), изги­бают балку выпуклостью вниз (растянуты нижние волокна балки), а моменты, изображен­ные на рисунках (б), изгибают балку выпуклостью вверх (растянуты верхние волокна балки). Это можно легко проверить, изгибая тонкую линейку.

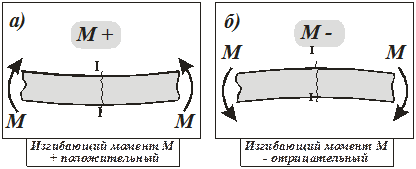
Отсюда следует другое, более удобное для запоминания правило знаков для изгибаю­щего момента. Изгибающий момент считается положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз. Волокна балки, расположенные в вогнутой части, испытывают сжатие, а в выпуклой – растяжение.

При построении эпюр поперечных сил положительные ординаты откладываются вверх от рассматриваемой оси балки. В отличие от поперечных сил, положительные ординаты для эпюр изгибающих моментов откладываются вниз (показывают растянутые волокна).

Известно, что деформация изгиба характеризуется тем, что в поперечных сечениях балки возникают изгибающие моменты, и, часто одновременно с последними – поперечные силы;

Изгиб называют чистым, если в сечениях балки возникают только изгибающие моменты.

Если же наряду с изгибающими моментами в сечениях балки возникают и поперечные силы, изгиб называют поперечным.

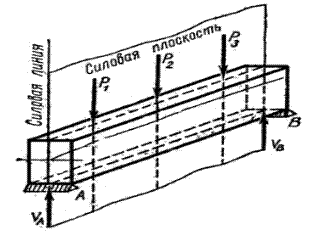
Деформация изгиба имеет место в результате действия внешних сил, приложенных перпендикулярно оси балки, а также от пар сил, плоскость действия которых проходит через ее ось.

Плоскости, в которых лежат главные центральные оси инерции поперечных сечений, называют главными плоскостями балки.

Дата добавления: 2013-12-12