Механические колебания

Движение, которое повторяется через равные промежутки времени, называется колебатель­ным. Промежуток времени T, по истечение кото­рого движение повторяется, называется перио­дом колебания. В моменты времени t и t + Т частица имеет одно и то же положение и одну и ту же скорость. Величина ν, обратная периоду, называется частотой: ν = 1/ Т. Она определяет, сколько раз в секунду повто­ряется движение, и измеряется в герцах (Гц). Круговой (циклической) частотой называ­ется величина ω = 2 π v.

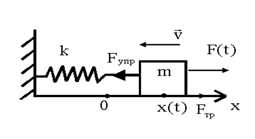
Свободные (собственные) колебания –колебания, происходящие без внешних воздей­ствий за счет первоначально полученной телом энергии. Рассмотрим горизонтальный пружинный маятник жесткостью k и массой m, помещенный в среду с коэффициентом сопротивления r, на который вдоль оси х действует переменная внешняя сила F(t), изменяющаяся со временем, например, по гармоническому закону F(t) = F₀ · cosΩt с некоторой частотой Ω.

Уравнение движения маятника:

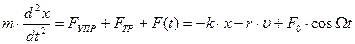(1), где сила упругости F_УПР пропорциональна смещению х, а сила трения (сопротивления) F_ТР среды – скорости υ= dx/dt. Перепишем (1) по другому:

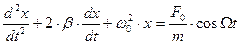(2),

где введены обозначения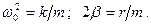

Проанализируем уравнение (2).

1. Свободные гармонические незатухающие колебания.

Маятник в отсутствие силы трения (r =0) и внешней силы (F₀= 0) отведен от положения равновесия и отпущен. Уравнение движения имеет вид:

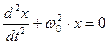(3).

Его решением является гармоническая функция: 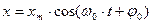(4),

в чем легко убедиться, подставив (4) в (3).

В (4) x_m, ω ₀ и φ₀ – постоянные величины. x_m – амплитуда – величина, указывающая максимальное значе­ние координаты х при отклонении от положения равновесия, ω ₀ – собственная частота, аргумент косинуса носит название фазы колебания; φ₀ — начальная фаза коле­бания (в момент t = 0).

Частота колебаний зависит только от свойств колеблю­щейся системы, но не от амплитуды, а амплиту­да и начальная фаза колебаний определяются начальными условиями ее движения, выводя­щими систему из состояния покоя.

Скорость колеблющейся частицы равна: 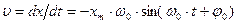(5).

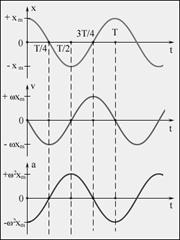
Ускорение частицы при таком движении: 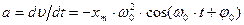(6). На рис. приведены зависимости x(t), υ(t) и a(t) для φ₀ =0.

Складывая кинети­ческую энергию с потенциальной, найдем полную энергию частицы, колеблющейся под действием упругой силы:

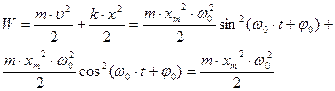(7).

Т.о., полная энергия пропорциональна квадрату амплитуды колебаний. Кинетическая и потен­циальная энергии изменяются со временем, как sin²(ω₀·t + φ₀) и cos²(ω₀·t + φ₀), так что когда одна из них увеличивает­ся, другая – уменьшается, т.е. процесс колеба­ний связан с периодическим переходом энергии из потенциальной в кинетическую и обратно. Сред­ние за период колебания значения потенциальной и кинетической энергии одинаковы и равны W/2. Т.о., если на тело действует сила, пропорциональная величине смещения час­тицы х и направленная в сторону, противоположную этому смещению (таковы, например, упругая сила, F=– k·x, действующая на пружинный маятник, или сила тяжести, действующая на математический или физический маятники), то оно совершает т.н. гармонические колебания (движение совершается по закону синуса или косинуса).

Примечание: В механике обычно рассматривают колебания: – математического маятника с периодом 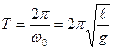, где ℓ– длина маятника;

– физического маятника с периодом 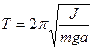, где J– момент инерции маятника, a – расстояние от точки подвеса маятника до его центра масс;

– пружинного маятника с периодом 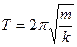, где k– жесткость пружины.

Дата добавления: 2013-12-12