Свободные затухающие колебания

При наличии силы трения (r ≠0) и отсутствии внешней периодической силы (F₀ = 0) уравнение движения имеет вид: 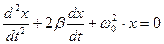(8),

где β называется коэффициентом затухания колебаний. В случае слабого затухания (β – мало) решением такого дифференциального уравнения является функция: 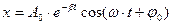(9). В этом можно убедиться прямой подстановкой (9) в уравнение (8). 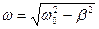– частота колебаний системы с затуханием. A=A₀·e^-βt – амплитуда затухающих колебаний.

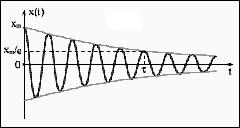
Таким образом, амплитуда колебаний убыва­ет по экспоненциальному закону. Вместе с амплитудой убывает также и энергия колебаний W, т.к. W~A².

Степень убывания амплитуды определяется коэффициен­том затухания β. Время τ=1/β, за которое амплитуда колебаний уменьшается в е=2.7183 раз, называют по­стоянной времени затухания колебаний.

Скорость уменьшения амплитуды за период характеризует величина θ, называемая лога­рифмическим декрементом затухания. По определению:

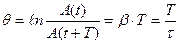(10).

Скорость убывания энергии в системе с зату­ханием характеризует добротность Q:

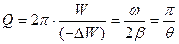(11),

где W – энергия, запасенная в системе, (– ΔW)– энергия, теряемая системой за период. Добротность показывает, во сколько раз энер­гия, запасенная в системе, больше энергии, те­ряемой за период. Добротность в (11) выражена через параметры системы и логарифмический декремент затухания θ, с учетом того, что W~A².

В случае сильного затухания (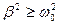) колебательный процесс не развивается: система, выведенная из состояния равновесия и предоставленная самой себе, просто медленно возвращается к нему. Это т.н. апериодический процесс.

Дата добавления: 2013-12-12