Механические волны

Явление распространения колебаний в про­странстве называется волновым движением или волной.

Уравнение волны выражает зависимость смещения Ψ колеблющейся точки, участвую­щей в волновом процессе, от ее координаты х и времени t.

Волна называется продольной, если колебания частиц происходят вдоль линии распространения вол­ны; если колебания частиц перпендикулярны к направлению распространения волны, то волна называется поперечной.

Геометрическое место точек, до которых к некоторому моменту времени дошло колеба­ние, называется фронтом волны. Можно так­же в среде выделить геометрическое место то­чек, колеблющихся в одинаковых фазах. Эта совокупность точек образует поверхность оди­наковых фаз или волновую поверхность. Фор­ма фронта волны определяет тип волн, напри­мер, у сферической волны фронт представляет собой сферу.

Скорость распространения волны есть скорость распространения данной фазы (волновой поверхности). Ее называют фазовой скоростью υ волны.

Расстояние, на которое определенная фаза колебания распространяется за один период Т колебания, называется длиной волны λ =υ· T.

Простейшим видом волн является плоская волна. Колебания частиц среды в ней происходят в плоскостях, перпендикулярных к направлению распространения. Если колебания в каждой точке следуют гармоническому зако­ну и происходят с одной частотой, то волна называется гармонической и монохромати­ческой.

Уравнение плоской волны, распространяю­щейся в положительном направлении оси х, имеет вид: 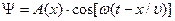(17),

где А(х) = A₀·e^-rx – амплитуда колебаний точек среды, расположенных на расстоянии x от источника колебаний (в среде без затухания А=А₀= const). Так как ω =2π/ T, то: 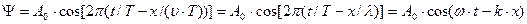(18).

Здесь k=2π/λ=2π/ (υ· T)=2πν/υ=ω/υназывается волновым чис­лом и является модулем волнового вектора 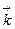, указывающего направление распространения волны.

Уравнение волны в виде (18) – одно из воз­можных решений общего дифференциального уравнения, описывающего распространение возмущения в среде. Это общее уравнение на­зывается волновым уравнением. Его можно получить, взяв от функции Ψ вторые производ­ные по х и t,: 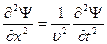(19),

где учтено, что в данном случае производные являются частными и сделана замена 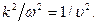Выражение (19) справедливо для волн любой природы.

Вещество вместе с волной не переносится. Частицы веще­ства только колеблются каждая около своего положения равно­весия. Колебания передаются вдоль направления распространения волны, вместе с ними передается и их энергия. Для описания этого процесса вводят вектор плотности потока энергии (вектор Умова) 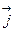, который направлен в сторону распространения волны, а его модуль равен энергии, переносимой волной через единицу площади за единицу време­ни.

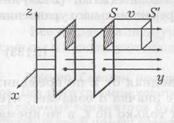
Выделим на фронте плоской волны (рис.) единичную площадку S. Через единицу времени фронт сместится на рас­стояние, равное скорости распространения волны υ и займет по­ложение S ’. Если в единице объема содержится энергия w (плотность энергии), то за единицу времени через сечение S ’= 1 пройдет вся энергия, заключенная в объеме между сечениями S и S ’, т. е. w·υ. Это и есть вектор Умова, если записать в векторной форме: 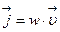. Он измеряется в Дж/(с·м²) или, что то же самое, в Вт/м². Эта фор­мула справедлива не только для механических волн, но и для волн любой природы, например электромагнитных.

Объемную плотность энергии w упругой волны получим, если рассмотрим в какой-либо области пространства колебание частиц среды объемом dV и массой dm=ρ·dV. Полная энергия колебаний этих частиц, согласно (7), будет равна:

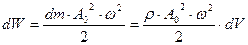(20),

где ρ – плотность вещества среды; ω – частота колебаний, А₀ – амплитуда колебаний.

Откуда следует, что: 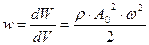(Дж/м³) (21).

.

В самом общем случае энергия волны, заключенная в некотором объеме V, согласно (21), рассчитывается по формуле: 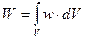(22).

Дата добавления: 2013-12-12