Магнитное поле, создаваемое проводом с током. Закон Био – Савара – Лапласа

Рамка с током в магнитном поле

На практике часто встречается такое использо­вание силы Ампера: между полюсами магнита по­мещают прямоугольную рамку из провода, по которому течет ток Используя правило левой руки, находим, что на левый участок провода действу­ет сила, направленная от нас, а на правый участок – к нам (рис.).

В результате рамка будет поворачиваться.

Механический момент силы, действующий на одну сторону рамки , на обе стороны . Поскольку в нашем случае с рамкой , можно просто написать М = 2·r·F или, воспользовавшись упрощенной формулой для силы Ампера,: M = 2·r·F = 2·r·I·ℓ·B = I·S·B, где S = 2 ·r·ℓ – площадь рамки.

Произведение I·S называется магнитным мо­ментом р_т рамки с током. Если рассматривать магнитный момент как вектор , направленный по нормали к плоскости рамки, то можно записать для : .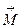

Если пропустить прямой провод с током I через лист фанеры, на котором насыпаны железные опилки, то окажется, что сило­вые линии 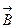около провода с током, вдоль которых располагаются маленькие магнитики-опилки, направлены всюду перпендикулярно этому току и представляют собой концентрические окружности (рис.). Их направление оп­ределяется по правилу правого буравчика.

Если ток круговой, то силовые линии со­здаваемого им поля будут такими, как показа­но на нижнем рисунке. Круговой ток – это элементарный магнит. Северным полюсом N магнита считается та сторона, откуда силовые линии выходят, южным S – куда силовые линии входят.

Био, Саваром и Лапласом было показано, что магнитное поле , создаваемое эле­ментом тока (I· 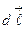) на рас­стоянии r, следует находить по формуле: , где 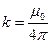– коэффициент пропорциональности, μ₀ = 4л·10^-7Гн/м – магнитная постоянная. Согласно этой формуле, поле зависит не только от величины тока, создающего поле, и расстояния до точки наблюдения, но и от взаимного расположения векторов (I· 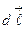) и 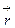, т. е. от угла α (рис.). Сравним это выражение с аналогичным в случае электростатического поля, где , создаваемое зарядом dq, находилось по формуле:, но там вектор был параллелен . 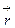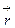В случае магнитного поля направление перпендикулярно и сильно зависит от угла α. Для магнитного поля также справедлив принцип суперпозиции: магнитное поле, созданное не­сколькими токами, равно векторной сумме маг­нитных полей, создаваемых каждым током в от­дельности: .

Поле в центре кругового тока (рис.).
Определяя направление в центре окружности, мы видим, что все векторы , создаваемые в этой точке всеми участками 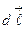, направлены одинаково (на рис. – от нас за чертеж). Следовательно, для нахождения обще­го 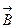можно просто все элементы dB складывать арифметически, так как для них α = 90°: .

Поле бесконечного прямого провода на расстоянии а от него (рис.). В этом случае все векторы , создаваемые всеми уча­стками 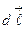в т.М, тоже направлены одинаково (от нас за чертеж), и их можно просто ариф­метически суммировать (интегрировать). Но теперь для каждого участка величины α и r будут разными. Для взятия интеграла удобнее все переменные свести к углу γ, провести интегрирование по γ от 0 до π/2 и результат удвоить: .

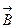Циркуляция вектора по замкнутому контуру

Определение циркуляции C_А некоторого вектора по замкнутому контуру ℓ уже давалось в разделе «Электростатика». Для 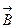она запишется так:

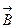, где θ – угол между и 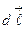(рис.).

Рассмотрим случай, когда контур охватывает ток I.

Будем для простоты считать, что магнитное поле созда­ется прямолинейным проводом с током I, направленным перпендикулярно рис. и от нас, т. е. в любой точке . При повороте на малый угол dφ: dx=a·dφ; dx/dℓ=cosθ. Подставив под знак интеграла, получим: .

Если замкнутый контур охватывает несколько токов, то под I понимается алгебраическая сумма токов и теорему о циркуляции вектора 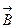можно сформулировать так: Циркуляция вектора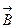равна алгеб­раической сумме токов, пронизывающих контур, умноженной на магнитную постоянную μ₀:.

Эту формулу удобно использовать для нахождения магнитной индукции В в различных случаях аналогично тому, как теорему Гаусса было удобно использовать для нахождения напряженно­сти электрического поля Е. Рассчитаем индукцию магнитного поля внутри тороида и длинного соленоида.

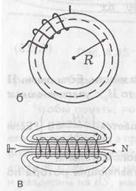
На рисунке б изображен тороид, на который намотано N витков провода с током I. Если выбрать контур по оси тороида (пунк­тир на рис.), где магнитное поле однородно, то: , откуда получим: . Из этого выражения найдем магнитную индукцию внутри длинной катушки – соленоиде, если ее рассматривать как часть очень большого тороида: B=μ₀·n·I, где – густота намотки.

Дата добавления: 2013-12-12