Квантовая теория атома

Уравнение Шредингера. Волны де Бройля описывают состояние только свободной частицы. В 1926 г. Э.Шредингер обобщил гипотезу де Бройля на случай движения микрочастицы во внешнем силовом поле и получил уравнение, описывающее поведение (распространение) волн вероятности во внешних силовых полях. Это уравнение, в результате решения которого получается конкретный вид ВФ, получи­ло название волнового уравнения,или уравнения Шредингера

Волновые свойства микрочастиц. Корпускулярно-волновой дуализм присущ не только свету, но и частицам вещества. Эту идею высказал, исходя из соображений симметрии, Луи де Бройль: если свет, который рассматривался как электромагнитная волна, может проявлять корпускулярные свойства, то и частицы вещества должны проявлять волновые свойства.

Согласно этой идее, импульс частицы с массой m и скоростью υ равен р = mυ, а с другой стороны, он равен p= h/λ. Следо­вательно, движущейся частице можно поставить в соответствие волну с длиной: λ_Б = h/p = h/mυ.

Величину λ_Б называют дебройлевской дли­ной волны частицы. Экспериментально волно­вые свойства микрочастиц были обнаружены в опытах по дифракции электронов на кристаллах.

Наличие волновых свойств у частиц вносит ограничения в применимости к ним классиче­ской механики, согласно которой час­тица в любой момент времени занимает опре­деленное положение в пространстве и обладает определенным импульсом.

Когда проводится какое-либо измерение, его результат содержит некоторую неопределен­ность, обусловленную двумя факторами: корпускулярно-волновым дуализмом и неизбеж­ным взаимодействием наблюдаемого объекта с регистрирующим прибором, приводящим к изменению состояния объекта. Поэтому сущест­вует предел, ограничивающий точность измерений. Этот предел не зависит от степени совершенства измерительного прибо­ра, а присущ самой природе вещей. Это и есть принцип неопределенностей Гейзенберга.

Количественные соотношения, выражающие этот принцип для конкретных динамических пе­ременных, называются соотношениями неопре­деленностей. Наиболее важными являются два из них:

.

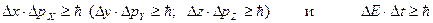Первое соотношение утверждает, что нельзя измерить одновременно с абсолютной точностью положение (координату) и проекцию импульса микрочастицы на ту же ось. Чем точнее мы пытаемся определить положение объекта, т.е. чем меньше Δ х, тем больше будет неопределенность импульса Δ р_x. Этот вывод можно понять из следующих рассуждений: пусть мы хотим как можно точнее узнать положение микрочастицы (Δ х→0). Для этого мы должны использовать фотоны с малой длиной волны λ (именно λ определяет точность измерения положения ∆х) и, соответственно, большим импульсом р_f = h/λ. В результате такого соударения двух частиц измеряемая частица приобретает непредсказуемый импульс. Если же мы попытаемся точно измерить проекцию импуль­са, то большой окажется неопределенность в по­ложении объекта. Принцип неопределенностей в то же время не запрещает точно определить что-то одно: либо положение, либо импульс. Можно так­же с абсолютной точностью измерить координату и проекции импульса на другие оси. Согласно этому соотношению неопределенностей: а) объяснена устойчивость атома; при гипотетическом падении электрона на ядро неопределенность положения электрона уменьшилась бы на 5 порядков с 10 ^–10 м (размер атома) до 10 ^–15 м (размер ядра). На 5 порядков соответственно увеличилась бы неопределенность импульса электрона и он, получив бы такую энергию, не смог бы удержаться в ядре; б) невозможно определить траекторию движения микрочастицы (для этого необходимо знать в каждый момент времени абсолютно точно и координату и импульс частицы);

Второе соотношение устанавливает связь между неопределенностью энергии Δ E квазистационарного возбужденного состояния и средним временем жизни Δ t возбужденного состояния в атомных процессах. Например, достаточно точно можно измерить энергию системы в стационарном состоянии, время жизни в котором велико (Δ t → ∞), если же система находится в нестационарном состоянии, время жизни Δ t в котором конечно, энергию можно измерить с погрешностью порядка Δ E ~ ħ /Δ t.

Волновая функция, физический смысл и свойства. Состояние квантовой частицы нельзя определять, как в классической механике одновременным заданием в каждый момент времени координат и импульса. Это запрещено принципом неопределенностей. По аналогии с электромагнитной волной, для которой электромагнитное поле определяется заданием некоторой функции координат и времени E(x,y,z,t), для описания движения микрочастиц вводится некоторая функция координат и времени Ψ(x,y,z,t), характеризующая волну де Бройля, и получившая название волновой функ­ции (ВФ).

Сама волновая функция Ψ в общем случае комплексна и поэтому не имеет наглядного физического представления, ее нельзя проде­монстрировать экспериментально. Согласно М.Борну, физический смысл имеет квадрат модуля ВФ 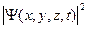, с помощью которого определяется вероятность dP того, что частица в момент времени t будет обнаружена в элементе объема dV, расположенном в окрест­ности точки х, у,z: .

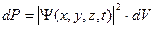Т.о, 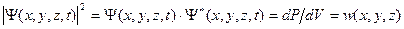, где Ψ ^* означает комплексно сопря­женную к Ψ величину, является плотностью веро­ятности.

Волну де Бройля можно рассматривать как волну вероятности, амплитудой которой является волновая функция.

Де Бройль постулировал, что свободное дви­жение частицы с определенной энергией E и импульсом 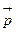описывается волновой функцией вида:

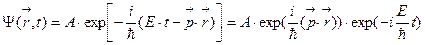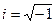. – мнимая единица.

Функция Ψ должна удовлетворять т.н. стандартным условиям. Она должна быть однозначной, поскольку микрочастица в определенный момент времени может находиться только в одной точке пространства. Волновая функция и ее частные производные по координатам являют­ся непрерывными во всех точках простран­ства (при движении частица не может исчезать в одном месте и появляться в другом). И наконец, волновая функция должна быть конечна, т.е. нигде не обращаться в бесконечность. Поскольку значение 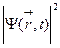, вычисленное в некоторой точке, пропорционально вероятности Р обнаружения частицы, описываемой функцией Ψ, в этой точ­ке, то интеграл от 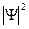по всему пространству должен быть конечным, так как в любом случае частица где-то должна быть. Обычно этот интеграл приравнивают единице: .

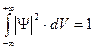Волновую функцию, для которой выполняет­ся это соотношение, называют нормирован­ной, а само равенство – условием норми­ровки волновой функции.

Нахож­дение вида волновой функции частицы, движущейся под действием внешних сил, является основной задачей квантовой механики, так как задание волновой функции есть полное и исчерпывающее описание этой частицы. Это связано с тем, что вероятностное пове­дение микрочастиц лежит в самой их природе.

,

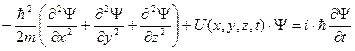где m – масса частицы, U(x,y,z,t) – потенциальная функция частицы в силовом поле.

Как и все основные уравнения физики (напри­мер, законы Ньютона, уравнения Максвелла), уравнение Шредингера не имеет вывода. Пра­вильность уравнения Шредингера и толкование смысла фигурирующей в нем волновой функции подтверждаются огромным опытным материа­лом современной физики.

То, что уравнение Шредингера содержит лишь первую производную от Ψ по времени, связано с выражением принципа причинности: если известна волновая функ­ция Ψ(x,y,z,0) частицы в начальный момент времени, то можно однозначно определить ее волновую функцию Ψ(x,y,z,t) в любые последующие моменты времени t > 0. Однако, точное знание ВФ для какой-либо точки пространства позволяет определить лишь вероятность обнаружения микрочастицы в этой точке.

Часто потенциальная функция U частицы яв­ным образом не зависит от времени и в этом случае она имеет смысл потенциальной энергии. Силы, дей­ствующие на частицу, а следовательно, и U(х,у,z) за­висят только от координат. В этих случаях уравнение Шредингера можно упрос­тить, исключив всякую зависимость от t. Это получается, если ВФ представить в виде произведения координатной и временной частей:

.

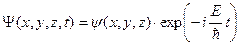Подставив в зависящее от времени уравне­ние Шредингера это выражение и сократив все уравнение затем на общий экспоненциаль­ный множитель, получим:

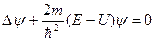, где 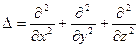- т.н. оператор Лапласа.

Это уравнение называется уравнением Шре­дингера для стационарных состояний.

Волновое уравнение Шредингера играет в квантовой механике ту же роль, что 2 закон Ньютона в классической механике. Задать закон движения частицы в квантовой механике – зна­чит определить Ψ -функцию в каждый момент времени в каждой точке пространства.

Так как уравнение Шредингера является урав­нением второго порядка в частных производ­ных, то для его решения необходимо задавать на­чальные и граничные условия.

Квантовая частица в потенциальной яме. Рассмотрим одномерное (вдоль оси х) движение частицы в потенциальном поле, называющемся беско­нечно глубокой прямоугольной потенциальной ямой шириной ℓ:

.

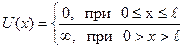Так как энергия частицы Е не может быть бес­конечной, частица не может находиться вне ямы, поэтому вероятность ее обнаружения вне ямы, а значит, и волновая функция, равна нулю: w (x <0)= w (x>ℓ) и ψ (x <0)= ψ (x>ℓ)=0.

Из условия непрерывности ВФ вытекает равенство нулю ВФ и на границе ямы: ψ(x=0)=ψ(x=ℓ)=0. Это граничные услови­я для решения уравнения Шредингера для частицы внутри потенциальной ямы: ,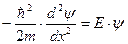

где Е — полная энергия частицы.

Решение такого дифференциального уравне­ния имеет вид:

ψ=A·sin(k·x), где 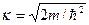- волновое число.

Используя граничное условие ψ(ℓ)=0, получим: κ_n ·ℓ=n·π,

где n =1,2,3,... – любое целое число, большее нуля (квантовое число). Еслиучесть, что импульс частицы p_n = ħ·k_n, то можнонайти возможные значения энергии частицы:

.

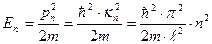Уравнение Шредингера имеет решения, удов­летворяющие граничным условиям только при дискретных значениях квантового числа п. Энер­гия частицы в бесконечно глубокой потенциаль­ной яме оказывается квантованной. Состояние частицы с наименьшей возможной энергией (n =1) называется основным, все остальные состоя­ния – возбужденными. Волновая функция, отвечающая n -му уров­ню энергии: 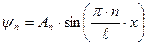. Постоянную А_n определим из условия нормировк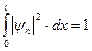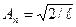и ; и .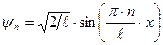

На границах ямы при х = 0 и х = ℓ всегда | ψ_n| ² = 0, однако, вeроятность нахождения частицы в определенной точке внутри ящика может сильно меняться при разных значениях квантового числа п.

Выводы: энергия микрочастицы, движущей­ся в потенциальной яме, пробегает дискретный ряд значений; даже в основном состоянии час­тица не находится в состоянии полного покоя; дискретный характер энергетических уровней проявляется при малой массе частиц и малых размерах области, в которой происходит движе­ние; при больших значениях квантовых чисел и пространственно неограниченном движении квантовомеханические соотношения переходят в формулы классической физики.

Квантовым гармоническим осциллятором называется микрочастица массы т, находящаяся в параболической потенциальной яме вида U(x)=κ·x²/2 и совершающая гармоническое движение с частотой ω; κ -постоянная.

Модель квантового ос­циллятора особенно полезна при исследова­нии малых колебаний систем около положения равновесия, например, колебаний атомов в уз­лах кристаллической решетки или колебаний атомов около их положений равновесия в мо­лекуле.

По аналогии с классической теорией (пружинный маятник) положим 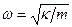. Тогда для потенциальной энергии по­лучим:

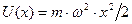. Стационарное уравнение Шредингера в дан­ном случае будет иметь вид:

.

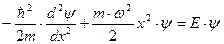Полученное уравнение имеет конечные, од­нозначные и непрерывные решения, т.е. собственные функции, не для всех значений энергии Е, а только при собственных значениях, удовлетворяющих условию: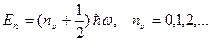

Число n_υ называется колебательным кванто­вым числом. Из последнего равенства следу­ет, что энергия квантового осциллятора кванту­ется. Энергетический спектр представляет собой эквидистантные, т.е. отстоящие друг от друга на одинаковую величину Δ E=ħω, уровни. Минималь­ная энергия, которой может обладать квантовый осциллятор, равна Е ₀ = ħω / 2 и называется энер­гией нулевых колебаний, или нулевой энергией и соответствует абсолютному нулю температур.

То, что минимальная энергия осциллятора не может быть равна нулю даже при 0К, находится в соответ­ствии с признанием относительности покоя и вечности движения. Если бы энергия частицы равнялась нулю, то это озна­чало бы, что частица покоится и ее импульс и координата одновременно имеют точные значения, что противоречит принци­пу неопределенностей. Существование нулевых колебаний доказы­вают опыты по наблюдению рассеяния света прозрачными кристаллами при сверхнизких (вплоть до 10 ^{– 6}К) температурах.

Расчет показывает, что для квантового осцил­лятора возможны переходы только между сосед­ними уровнями, т.е. с изменением квантового числа n_υ на единицу:

Δ n_υ = ±1.

Это условие называется правилом отбора, оно показывает, какие из всех мыслимых переходов реализуются в действительности.

При каждом из переходов излучается или по­глощается фотон (или другая частица – фонон) с энергией ħω, где ω – его цик­лическая частота.

Оптические атомные спектры. Известно, что в излучении нагретых тел представлены все длины волн (сплошной спектр).

Если нагреть до достаточно высокой темпе­ратуры атомарный газ, то в спектре его излуче­ния (спектре испускания) появляются яркие светящиеся линии с определенными дискретными длинами волн. Такие спектры называются линейчатыми. Каждый химический элемент обладает собственным линейчатым спектром.

Простейшим является атом водоро­да: он состоит из протона и электрона. У водорода самый простой спектр. Дж. Бальмер при изучении видимой части спектра водорода обнаружил четыре спектраль­ные линии с частотами 4,552; 6,173; 6,912 и 7,317 (в 10¹⁴ с^-1) и показал, что частоты этих линий могут быть рассчитаны по формуле: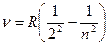, где для первых четырех линий n принимает зна­чения 3, 4, 5 и 6. R= 3,29·10¹⁵ c^-1 - постоянная Ридберга, была определена экспериментально. Впоследствии были обнаружены линии, соответствующие другим значениям п> 6.

Установлено, что по мере увеличения частоты линии располагают­ся все ближе и ближе друг к другу и становятся все менее интенсивными. Вблизи линии с частотой 0,8242·10¹⁵ с^-1 линии сгущаются настолько, что их трудно различить. Эта частота, соот­ветствующая п=∞, называется границей серии, после нее уже не наблюдается отдельных линий, а имеется слабо выраженный сплошной спектр.

Совокупность спектральных линий, обнаружи­вающих в своей последовательности и в рас­пределении интенсивности описанную выше закономерность, называется спектральной серией.

Наряду с серией Бальмера в спектре атома водорода был обнаружен ряд других серий, представляемых совершенно аналогичными формулами:

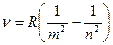, m =1,2,3,… n=m+1,m+2,… Это т.н. обобщенная формула Бальмера.

В ультрафиолетовой области Лайман открыл серию линий, частоты которых соответству­ют значению m = 1.

В инфракрасной области были обнаружены другие спектральные серии (серии Пашена m = 3, Брэкета m =4, Пфунда m = 5 и т.д.).

Вид этих формул, дискретность частот, определяемую целыми числами n и m, не смогла объяснить классическая физика.

Боровская модель атома водорода. Спектральные серии и устойчивость атома водорода Н.Бор объяснил на основе двух постулатов:

Дата добавления: 2013-12-12