Свободная энергия Гельмгольца. Свободная энергия Гиббса

Второе начало термодинамики для обратимых и необратимых процессов. Объединенное уравнение первого и второго начал термодинамики

Для обратимых процессов справедливо выражение

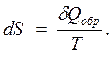(2.35)

Уравнение представляет собой математическую формулировку второго начала термодинамики для обратимых процессов.

В изолированных системах:

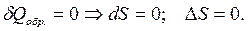(2.36)

Если процесс совершается при конечном изменении состояния системы, то

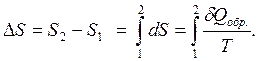(2.37)

Полное приращение энтропии в обратимом круговом процессе равно нулю

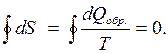- равенство Клаузиуса (2.38)

Для обратимых процессов второе начало термодинамики представляет собой закон о существовании и сохранении энтропии. При обратимых процессах в изолированной системе энтропия остается постоянной.

Если обратимые процессы происходят в неизолированной системе, то энтропия системы может изменяться с изменением энтропии окружающей среды, причем таким образом, чтобы сумма энтропии оставалась постоянной.

Иногда энтропию называют мерой беспорядка: чем меньше упорядочено вещество, тем выше его энтропия. Энтропия возрастает с увеличением температуры.

Следствием из второго начала термодинамики является то, что работа любого необратимого процесса всегда меньше работы обратимого процесса между одними и теми же начальным и конечным состояниями,т.е.

А_необр < А_обр,

δА_необр < А_обр (2.39)

Поэтому работа в обратимом процессе называется максимальной работой; чем меньше работа по сравнению с максимальной, тем более необратим процесс. Процессы, происходящие без совершения работы, являются полностью необратимыми.

Энтропияявляется критерием равновесия и самопроизвольности только тех процессов, которые идут в изолированных системах, т.е. (U,V=const). Химические процессы обычно протекают либо при постоянном объеме и температуре (закрытые системы), либо при постоянном давлении и температуре (открытые системы).

В изобарно-изотермических условиях движущей силой процесса является стремление системы уменьшить энергию, т.е. выделить тепло в окружающую среду.

ΔН<0 или рост S - DS>0– критерий самопроизвольности.

Если ΔН=0, то рост энтропии является единственной движущей силой и наоборот при DS=0 – движущей силой является убыль Н.

Требования U,V=const исключает использование S как критерия направления и протекания процессов при которых U и V меняются. Но с помощью энтропии можно вычислить другие термодинамические функции, которые являются более подходящими критериями оценки состояний системы.

Поэтому в качестве критерия направления и протекания процессов введены термодинамические функции включающие энтропию.

F = U – TS;

G = H – TS. (2.48)

Функции F и G называются соответственно свободной энергией Гельмгольца (изохорно-изотермический потенциал) и свободной энергией Гиббса (изобарно-изотермический потенциал). TS характеризует связанную энергию, которая не может быть превращена в работу в изотермическом процессе, а лишь переходит в тепло.

F и G являются функциями состояния, так как выражаются через функции состояния. Эти функции используются как критерии равновесия и направления процесса в системе:

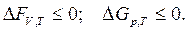(2.49)

Из выражений следует, что ΔF и ΔG остаются постоянными для обратимых процессов и уменьшаются для необратимых. Обратимые процессы протекают т.о., что при возврате системы в исходное состояние никаких изменений в окружающей среде не происходит. При необратимых процессах систему нельзя вернуть в исходное состояние.

Равновесное состояние системы описывается выражением

ΔF_V,Т = 0, ΔG_р,T = 0. (2.50)

В состоянии равновесия при постоянном объеме и температуре энергия Гельмгольца, а при постоянном давлении и температуре энергия Гиббса минимальны.

Изменение трех критериев равновесия и направления процесса в системе, а именно S, F и G, можно изобразить следующим образом (рис.2.3):

U,V=const V,T=const р,Т=const

S В F A G A

А B B

Ход процесса

Рис. 2.3.

т. В – состояние равновесия, сплошной участок – самопроизвольный процесс.

В состоянии равновесия энтропия максимальна, а свободные энергии Гельмгольца и Гиббса имеют минимум.

Т.о. при р,Т=const реакция протекает самопроизвольно в направлении уменьшения D G, а при V,T=const в в направлении уменьшения D F.

Изменение этих функций для химических процессов вычисляется по формулам

D F = DU – TDS; DG = DH - TDS. (2.51)

Рассмотрим изменение DG при изменении DH и DS

DH DS DG

<0 >0 <0 протекает самопроизвольно при любых Т;

<0 <0 <0 протекает самопроизвольно низких Т;

>0 >0 <0 протекает самопроизвольно высоких Т;

>0 <0 >0 протекает самопроизвольно обратный процесс.

Чем < DG, тем дальше система от состояния равновесия и тем более реакционноспособна. При равновесии DG=0 и DН= ТDS.

Дата добавления: 2013-12-12