Способы перенесения точек проекта в натуру

Перенесение проектов сооружений в натуру осуществляется способами прямоугольных координат (перпендикуляров), полярных координат, линейных и угловых засечек, створных засечек.

Способ прямоугольных координат (рис. 3.4.1.). Проектные точки А и В определяют в натуре, строя перпендикуляры от створа линии геодезического обоснования MN в точках P и Q, а на перпендикулярах откладывая ординаты У_A и У_B.

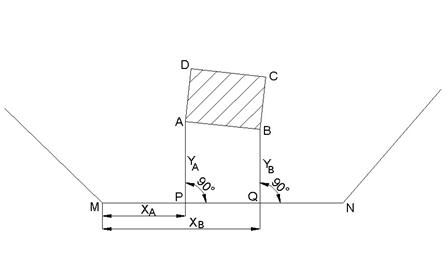
Рис. 3.4.1. Схема разбивки сооружений способом перпендикуляров

Способ полярных координат (рис. 3.4.2.). Положение проектных точек А и В в натуре определяют строя в пунктах геодезического обоснования М и N углы b₁ и b₂ и откладывая расстояния d_A и d_B.

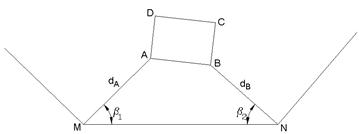
Рис. 3.4.2. Схема разбивки сооружений способом полярных координат

Способ прямой угловой засечки (рис. 3.4.3.). Определение положения точек А и В осуществляется путем построения углов b₁ и b₂, b₃ и b₄, образованных исходной стороной MN геодезического обоснования и направлениями с его конечных пунктов М и N на определяемые точки А и В. Углы засечки должны быть не менее 30° и не более 150°.

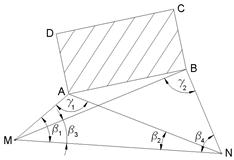
Рис. 3.4.3. Схема разбивки сооружений способом угловой засечки

Способ прямой угловой засечки применяется при перенесении на местности точек проекта, расстояние до которых измерить затруднительно или невозможно.

Для перенесения в натуру точки A этим способом необходимо отыскать на местности опорные точки M и N, знать величины разбивочных углов β ₁ и β ₂. Разбивочные углы β ₁ и β ₂ вычисляют как разность дирекционных углов, образованных исходной стороной и направлениями с ее конечных точек M и N на определяемую точку A.

Рис. 3.4.4. Схема построения створов в способе угловой засечки

По известным координатам опорных пунктов M и N и точки A решением обратной геодезической задачи вычисляют дирекционные углы соответствующих направлений. При этом пользуются формулами:

;

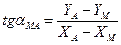(3.4.1.)

.

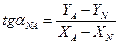По дирекционным углам направлений вычисляют углы β ₁ и β ₂:

;

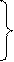
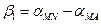. (3.4.2.)

Положение точки A на местности определяют построением на местности с помощью теодолита углов β ₁ и β ₂ на пересечении линий MA и NA.

Из точек M и N строят углы β ₁ и β ₂, а около А замечают сначала вспомогательные точки m ₁ и m ₂, потом n ₁ и n ₂ (рис. 3.4.4.). По натянутым шнурам устанавливают точку A. Углы строят как одним, так и двумя теодолитами одновременно. При этом соблюдают условие 30°<γ<150°. Наиболее точную засечку получают при γ≈110°.

Способ линейных засечек (рис. 3.4.5.). Положение точек А и В определяют пересечением дуг, описанных радиусами d₁ и d₂, d₃ и d₄, из точек геодезического обоснования M, P, Q, N. Длину радиусов берут с плана или вычисляют по координатам. Расстояние от определяемых точек А и В до пунктов геодезической основы не должно превышать длины мерного прибора, т. е. 20 – 25 м.

Способ створной засечки и створно-линейной засечки (рис. 3.4.6.). В способе створной засечки искомая точка P определяется пересечением двух створов, задаваемых между исходными точками 1 – 1^/ и 2 – 2^/. Створы можно строить с помощью двух теодолитов или с помощью тонких проволок.

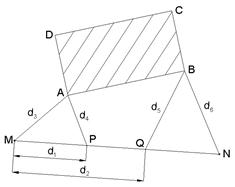
Рис. 3.4.5. Схема разбивки сооружений способом линейной засечки

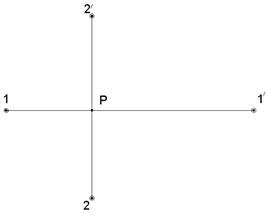
Рис. 3.4.6. Схема разбивки сооружений способом створной засечки

Створно-линейный способ позволяет определить проектное положение выносимой в натуру точки P путем отложения проектного расстояния d по створу 1 – 1^/.

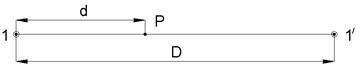
Рис. 3.4.7. Схема разбивки сооружений способом створно-линейной засечки

Дата добавления: 2013-12-12