И их свойства

Базис. Координаты вектора в данном базисе

Базис. Координаты вектора

Множество всех векторов, на котором введена операция сложения векторов, удовлетворяющая свойствам

1⁰. ;

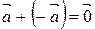2⁰. ;

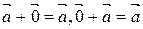3⁰. ;

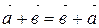4⁰. ,

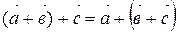и операция умножения вектора на число, удовлетворяющая свойствам

1⁰. , ;

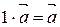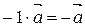2⁰. ;

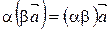3⁰. ;

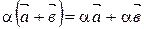4⁰. ,

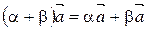называется векторным пространством и обозначается через V.

Базисом векторного пространства называется система векторов, заданных в определенном порядке, которая удовлетворяет условиям:

1) система линейно независима;

2) любой вектор пространства является линейной комбинацией данной системы векторов.

Число векторов базиса называется размерностью векторного пространства.

Выяснить, чему равна размерность векторного пространства V, позволяют следующие две теоремы, которые приведем без доказательства:

Теорема 1. Любая система трех некомпланарных векторов, взятых в определенном порядке, образует базис векторного пространства.

А может ли базис пространства V состоять меньше, чем из трех векторов? Больше, чем из трех векторов? Оказывается, нет, так как справедлива

Теорема 2. Любой базис векторного пространства V состоит из трех векторов.

Эти теоремы можно доказать, пользуясь теоремами о коллинеарных и компланарных векторах и свойствами 2⁰ - 7⁰ линейно зависимой системы векторов.

Из теорем 1 и 2 следует, что размерность векторного пространства V равна 3, поэтому оно называется трехмерным векторным пространством.

Базис, состоящий из векторов 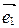, 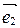и 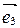, обозначается так: 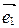, , 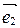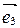или 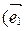, , 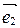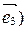. Векторы 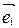, , 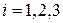называются базисными векторами: 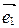- первый базисный вектор, 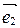- второй, 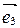- третий.

Пусть 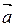- произвольный вектор пространства V, 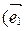, , 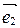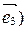- базис векторного пространства V.

Из теоремы 1 следует, что вектор 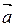можно разложить по базисным векторам 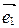, , 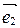, 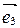т.е. существуют такие действительные числа 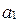, , 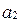, 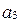что

.

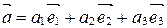Коэффициенты 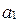, , 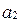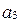в этом разложении называются координатами вектора 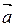в базисе 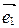, , 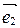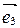: 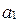- первая координата, 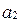- вторая, 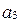- третья.

Обозначают это так: (;;) _,,.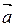

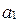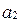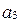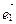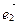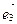Когда ясно, о каком базисе идет речь, пишут так: (;;).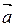

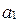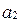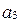Дата добавления: 2013-12-12