В математике выражение вида

Сравнение выражений (1.9) и (1.10) приводит к соотношениям

(1.11)

Таким образом, компоненты скорости равны производным соответствующих координат по времени.

Зная модуль скорости в каждый момент времени, можно вычислить путь, пройденный частицей от момента времени t₁ до момента t₂. Разобъем интервал времени t₂-t₁ на N малых (не обязательно одинаковых) промежутков Dt_i (i- номер промежутка, который пробегает значения 1, 2, 3,….N). В соответствии с формулой (1.7) можно считать, что путь Ds_i, пройденный частицей за время Dt_i, приближенно равен произведению v_i на Dt_i:

Ds_i»v_iDt_i (1.12)

(здесь v_i-какое-либо значение скорости из промежутка Dt_i). Весь путь s, пройденный частицей, равен сумме путей Ds_i:

s=Ds₁+Ds₂+…+Ds_N=. (1.13)

(мы воспользовались сокращенной записью суммы). Заменив в (1.14) Ds_i его приближенным значением (1.12), получим

s». (1.14)

Если уменьшать промежутки времени Dt_i, произведения v_iDt_i с возрастающей точностью будут определять пройденные за эти промежутки пути Ds_i. Поэтому, сделав предельный переход, при котором все Dt_i стремятся к нулю (N при этом неограниченно возрастает) мы получим точное значение пути:

s=. (1.15)

s=, (1.16)

составленное для значений х, заключенных в пределах от а до b, называют определенным интегралом от функции f(x), взятым по переменной х между нижним пределом х=а и верхним пределом х=b, и обозначают символом

. (1.17)

Сравнение выражений (1.15) и (1.16) показывает, что путь, пройденный частицей за промежуток времени от t₁ до t₂, равен определенному интегралу от функции v(t), показывающей, как изменяется модуль скорости с течением времени:

s=. (1.18)

Определенный интеграл имеет простой геометрический смысл. На рис.1.4 видно, что произведение v_i Dt_i приближенно равно площади полоски с основанием Dt_i. Сумма таких произведений, т.е. выражение (1.15), приближенно равно площади фигуры, ограниченной кривой v(t). При дроблении полосок на более узкие (что соответствует процессу, при котором все Dt_i®0) сумма площадей полосок переходит в площадь фигуры, ограниченной снизу осью t, с боков – прямыми t=t₁ и t=t₂, а сверху – графиком функции v(t). Эта

площадь численно равна определенному интегралу (1.18).

С учетом выражения (1.18) среднее значение модуля скорости можно представить в виде

<v>= (1.19)

(время движения t=t₂-t₁). Геометрический смысл <v> ясен из рис.1.5.

Аналогично вычисляются средние значения любых скалярных или векторных функций. Например, среднее значение функции у(х) на промежутке от х₁ до х₂ определяется выражением

<y>=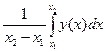. (1.20)

Среднее значение скорости за время от t₁ до t₂ равно

< v >= (1.21)

(заметим, что векторную функцию нельзя изобразить в виде графика, поэтому рис.1.4 и 1.5 к данному интегралу неприменимы.) Согласно формуле (1.5) v (t)dt=d r есть перемещение частицы за время dt. Следовательно, можно написать, что

< v >=

t₁

(1.22)

где r₁₂ – перемещение частицы за промежуток времени t₂-t₁.

Дата добавления: 2013-12-11