Закон сохранения момента импульса

Рис. 7.1). Плечом силы называют длину перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила. Направлен вектор М перпендикулярно к плоскости, в которой лежат сила и точка О, причем так, что направление вращения, обусловленного силой, и направление вектора М образуют правовинтовую систему (поворот головки винта или шурупа с правой нарезкой в направлении силы вызвал бы перемещение винта в направлении вектора М). Поскольку его направление определяется условно, М является псевдовектором.

Момент силы

Лекция 7

Моментом силы относительно точки О называется вектор М, модуль которого равен произведению модуля силы на ее плечо l:

М=Fl=Fr sina (7.1)

На рис. 7.1 вектор М изображен в виде кружка с крестиком внутри. Так мы будем в дальнейшем обозначать векторы, перпендикулярные к плоскости чертежа и направленные «от нас». Векторы, перпендикулярные к плоскости чертежа и направленные «на нас», мы будем обозначать кружком с точкой внутри него.

Момент силы можно представить в виде векторного произведения радиус –вектора r точки приложения силы на силу F.

М =[ rF ] (7.2)

Здесь r – радиус-вектор точки приложения силы, проведенной из точки, относительно которой определяется момент.

Когда сила приложена к одной из точек твердого тела, вектор М характеризует способность силы вращать тело вокруг точки О, относительно которой он берется. Поэтому момент силы называют также вращающим моментом. Если тело может вращаться вокруг точки О произвольным образом, то под действием силы тело повернется вокруг оси, совпадающей с направлением вращающего момента.

Проекция вектора М на произвольную ось z, проходящую через точку О, называется моментом силы относительно этой оси:

М_z=[ rF ]_пр.z. (7.3)

Разложим силу F на три составляющие, как показано на рис. 7.2. Воспользовавщись дистрибутивностью векторного произведения, представим момент силы F относительно точки О в виде

М =[ r, (F _II+ F _^+ F _i)]=[ rF _II]+[ rF _^]+[ rF _i]= M _II+ M _^+ M _i,

где М _II – момент силы F _II и т.д.

Проекция на ось z вектора М равна сумме проекций моментов составляющих сил. Моменты М _II и М _^ перпендикулярны к оси z, поэтому их проекции равны нулю. Следовательно,

М_z=(М_i)_пр.z=М_i cosa=rF_i cosa=RF_i (7.4)

(Рис. 7.2)

Из трех составляющих силы F вращение вокруг оси z может вызвать только сила F_i, причем она тем успешнее осуществит этот поворот, чем больше ее плечо R относительно точки О^I. Таким образом, момент силы относительно оси характеризует способность силы вращать тело вокруг этой оси.

Две равные по модулю противоположно направленные силы, не действующие вдоль одной прямой, называют парой сил (рис.7.3). Расстояние l между прямыми, вдоль которых действуют силы, называется плечом пары. Суммарный момент сил относительно точки О равен

М =[ r₁F₁ ]+[ r₂F₂ ].

Учтя, что F ₂=- F ₁, можно написать

М =[ r₁F₁ ]-[ r₂F₁ ]=[(r ₁- r ₂), F ₁]=[ r ₁₂ F ₁] (7.5)

где r ₂₁= r ₁- r ₂ (рис.7.3). Полученное выражение не зависит от положения точки О, следовательно, момент пары сил относительно любой точки будет одним и тем же. Вектор М перпендикулярен к плоскости, в которой лежат силы, а его модуль равен произведения модуля любой из сил на плечо.

Силы гравитационного и кулоновского взаимодействия между двумя частицами образуют пару с плечом, равным нулю. Поэтому их суммарный момент относительно любой точки равен нулю. Отсюда следует, что моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы частиц всегда равна нулю:

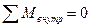(7.6)

Соответственно равен нулю и суммарный момент относительно любой оси z:

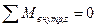. (7.7)

По аналогии с моментом силы, моментом импульса материальной точки (частицы) относительно точки 0 называется векторная величина

L =[ rp ]=[ r, mv ], (7.8)

где r – радиус-вектор, определяющий положение частицы относительно точки 0, а р = mv – импульс частицы. Модуль этой величины, равный r p sina, можно представить в виде произведения плеча l импульса на модуль вектора р:

L=l p (7.9)

(рис. 7.4)

Частица обладает моментом импульса, независимо от формы траектории, по которой она движется. Рассмотрим два частных случая.

1. Частица движется вдоль прямолинейной траектории (рис.7.5). Модуль момента импульса

L=mvl (7.10)

может изменяться только за счет изменения модуля скорости.

2. Частица движется по окружности радиуса r (рис. 7.6). Модуль момента импульса относительно центра окружности равен

L=mvr (7.11)

и так же, как в предыдущем случае, может изменяться только за счет модуля скорости. Несмотря на непрерывное изменение направления вектора р, направление вектора L остается постоянным.

Проекция вектора L на произвольную ось z, проходящую через точку 0, называется моментом импульса частицы относительно этой оси:

L_z=[rp]_пр.z, (7.12)

Выясним, от чего зависит изменение момента импульса частицы. С этой целью продифференцируем выражение (7.8) по времени:

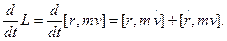
Согласно второму закону Ньютона m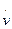=F – результирующей сил, действующих на частицу; по определению 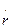=v. Поэтому можно написать, что

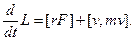
Второе слагаемое является векторным произведением коллинеарных векторов и поэтому равно нулю. Первое слагаемое представляет собой момент силы F относительно той же точки, относительно которой взят момент импульса L. Следовательно, мы приходим к соотношению

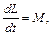(7.13)

согласно которому скорость изменения момента импульса со временем равна суммарному моменту сил, действующих на частицу.

Спроектировав векторы, фигурирующие в уравнении (7.13), на произвольную ось z, проходящую через точку 0, получим соотношение

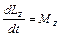. (7.14)

Таким образом, производная по времени от момента импульса относительно оси равна моменту относительно той же оси сил, действующих на частицу.

Рассмотрим систему частиц, на которые действуют как внутренние, так и внешние силы. Моментом импульса L системы относительно точки 0 называется сумма моментов импульса L_i отдельных частиц:

L =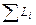= 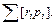(7.15)

Дифференцирование по времени дает, что

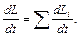(7.16)

В соответствии с (7.13) для каждой из частиц можно написать равенство

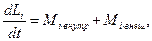
где М_{i внутр}- момент внутренних сил, М_{i внеш}- момент внешних сил, действующих на

i-ю частицу. Подстановка этих равенств в (7.16) приводит к соотношению

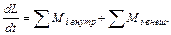
Каждое из слагаемых в этих суммах представляет собой сумму моментов сил, действующих на i-ю частицу. Суммирование осуществляется по частицам. Если перейти к суммированию по отдельным силам, независимо от того, к какой из частиц они приложены, индекс i в суммах можно опустить.

Суммарный момент внутренних сил равен нулю. Поэтому получаем окончательно, что

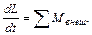(7.17

Спроектировав векторы, фигурирующие в формуле (7.17) на произвольную ось z, проходящую через точку 0, придем к уравнению

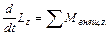(7.18)

Если система замкнута (т.е. внешних сил нет), правая часть равенства (7.17) равна нулю и, следовательно, вектор L не изменяется со временем. Отсюда вытекает закон сохранения момента импульса, который гласит, что момент импульса замкнутой системы материальных точек остается постоянным. Разумеется, будет оставаться постоянным и момент импульса замкнутой системы относительно любой оси, проходящей через точку 0.

Момент импульса сохраняется и для незамкнутой системы, если сумма моментов внешних сил равна нулю. Согласно (7.18) сохраняется момент импульса системы относительно оси z при условии, что сумма моментов внешних сил относительно этой оси равна нулю.

В основе закона сохранения момента импульса лежит изотропия пространства, т.е. одинаковость свойств пространства по всем направлениям. Поворот замкнутой системы частиц без изменения их взаимного расположения (конфигурации) и относительных скоростей не изменяет механических свойств системы. Движение частиц друг относительно друга после поворота будет таким же, каким оно было бы, если бы поворот не был осуществлен.

Плоское движение твердого тела

Плоским называется такое движение, при котором все точки тела движутся в параллельных плоскостях. Произвольное плоское движение можно представить как совокупность поступательного движения и вращения (рис. 7.7). Разбиение движения на поступательное и вращательное можно осуществить множеством способов (на рис. 7.7 показаны три из них), отличающихся значениями скорости поступательного движения, но соответствующих одной и той же угловой скорости w. Поэтому можно говорить об угловой скорости вращения твердого тела, не указывая, через какую точку проходит ось вращения.

Положим скорость поступательного движения равной v₀. Примем одну из точек, лежащих на оси вращения, за начало координат О. Согласно формуле

v =[ wr ]

составляющую скорости точек тела, обусловленную вращением, можно представить в виде [wr], где r – радиус-вектор, проведенный из точки О в данную точку тела. Следовательно, для скорости точек тела относительно неподвижной системы отсчета получается формула

v = v ₀+[ wr ] (7.19)

Особенно удобным оказывается разбиение произвольного плоского движения на поступательное, происходящее со скоростью центра масс v _с, и вращение вокруг оси, проходящей через этот центр (рис. 7.7 б).

Элементарное перемещение твердого тела при плоском движении всегда можно представить как поворот вокруг так называемой мгновенной оси вращения (рис. 7.7 а). Эта ось может находиться внутри либо вне тела. Положение мгновенной оси относительно неподвижной системы отсчета и относительно тела, вообще говоря, изменяется со временем. В случае, изображенном на рис. 7.7, мгновенная ось совпадает с линией касания цилиндра с плоскостью (ось А). Эта ось перемещается как по плоскости (относительно системы отсчета), так и по поверхности цилиндра. Таким образом, плоское движение можно рассматривать как ряд последовательных элементарных вращений вокруг мгновенных осей.

Дата добавления: 2013-12-11