
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доверительный интервал для математического ожидания нормального распределения при известной дисперсии
|
|
|
|
Дано: случайная величина x распределена по нормальному закону, для которого известна дисперсия s 2.
Делается выборка объема n. Вычисляем  . Покажем, что M
. Покажем, что M  = a и D
= a и D  =
= .
.
Выборка x 1, x 2,..., xn рассматривается как совокупность n независимых случайных величин, распределенных так же как x, следовательно,
Mx 1 = Mx 2 =... = Mxn = а Dx1 = Dx2 =... = Dxn = σ2.
 также случайная величина и распределена по нормальному закону в силу теоремы — сумма нормально распределённых случайных величин распределена по нормальному закону.
также случайная величина и распределена по нормальному закону в силу теоремы — сумма нормально распределённых случайных величин распределена по нормальному закону.
М  =М (
=М ( ) = M (
) = M (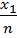 +
+  + … +
+ … +  ) = M (
) = M (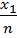 ) + M (
) + M ( ) + … + M (
) + … + M ( ) =
) =  M (
M ( ) =
) =  . n . a = a
. n . a = a
D  = D (
= D (
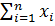 ) =
) = 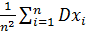 =
= 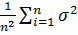 =
= 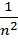 . n . σ2 =
. n . σ2 =  .
.
Итак,  → N (a;
→ N (a;  ).
).
Подберем по заданной надежности g число δ > 0 так, чтобы выполнялось условие:
P (|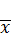 – a | < δ) = g. (1)
– a | < δ) = g. (1)
Так как случайная величина 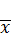 распределена по нормальному закону с математическим ожиданием a и дисперсией s 2 /n, получаем:
распределена по нормальному закону с математическим ожиданием a и дисперсией s 2 /n, получаем:
P (|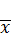 – a | < δ) = P (a – δ <
– a | < δ) = P (a – δ < 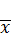 < a + δ) =
< a + δ) =
=  + Ф
+ Ф  –
–  + Ф
+ Ф 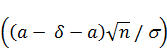 = 2 Ф
= 2 Ф 
2 Ф  = g, Ф
= g, Ф 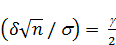 .
.
Обозначим  =
=  . Функция Ф (x) непрерывна и возрастает на интервале [ 0; +∞) от 0 до 0,5, поэтому для любого числа g Î[0;1] существует единственное число
. Функция Ф (x) непрерывна и возрастает на интервале [ 0; +∞) от 0 до 0,5, поэтому для любого числа g Î[0;1] существует единственное число  такое, что F (
такое, что F ( )= g / 2. Это число
)= g / 2. Это число  называют квантилем нормального распределения, и в конкретных примерах оно подбирается по таблицам нормального распределения функции Лапласа.
называют квантилем нормального распределения, и в конкретных примерах оно подбирается по таблицам нормального распределения функции Лапласа.
Теперь из равенства  =
=  определим значение
определим значение 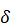 :
: 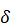 =
= 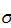

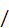
 . Окончательный результат получим, представив формулу (1) в виде:
. Окончательный результат получим, представив формулу (1) в виде:
P (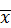

 < a <
< a < 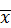

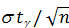 ) = g.
) = g.
Другими словами, с надежностью g доверительный интервал
(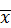

 ;
;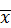

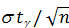 )
)
покрывает неизвестное значение параметр a = Mx генеральной совокупности. Можно сказать иначе: точечная оценка 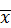 даёт значение параметра Mx с точностью
даёт значение параметра Mx с точностью 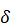 =
= 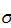

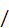
 и надежностью g.
и надежностью g.
Задача 1. Пусть имеется генеральная совокупность, распределенная по нормальному закону с дисперсией s 2, равной 6,25. Произведена выборка объема n = 27 и получено средневыборочное значение 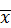 = 12. Найти доверительный интервал, покрывающий неизвестное математическое ожидание исследуемой характеристики генеральной совокупности с надежностью g =0,99.
= 12. Найти доверительный интервал, покрывающий неизвестное математическое ожидание исследуемой характеристики генеральной совокупности с надежностью g =0,99.
Решение. Сначала по таблице для функции Лапласа найдем значение  из уравнения F (
из уравнения F ( ) = g / 2, F (
) = g / 2, F ( ) = 0,495. По полученному значению
) = 0,495. По полученному значению  = 2,58 определим точность оценки
= 2,58 определим точность оценки 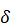 = 2,5´2,58 /
= 2,5´2,58 / 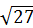 » 1,24. Отсюда получаем искомый доверительный интервал:
» 1,24. Отсюда получаем искомый доверительный интервал:
θ 1 = 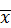

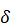 = 12
= 12  1,24 = 10,76
1,24 = 10,76
θ 2 = 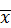

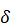 = 12
= 12  1,24 = 13,24, (10,76; 13,24).
1,24 = 13,24, (10,76; 13,24).
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 844; Нарушение авторских прав?; Мы поможем в написании вашей работы!