
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии
|
|
|
|
Пусть x – случайная величина, распределенная по нормальному закону с неизвестным математическим ожиданием a. Произведем выборку объема n. Вычислим среднюю выборочную  и исправленную выборочную дисперсию s 2.
и исправленную выборочную дисперсию s 2.
Случайная величина t = (
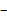 a)
a)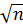 / s распределена по закону Стьюдента с (n – 1) степенями свободы.
/ s распределена по закону Стьюдента с (n – 1) степенями свободы.
Задача заключается в том, чтобы по заданной надежности g и по числу степеней свободы (n – 1) найти такое число tg,n, чтобы выполнялось равенство
P (|(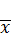 – a)
– a)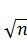 / s | < tg,n) = g (2)
/ s | < tg,n) = g (2)
или эквивалентное равенство
P (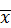 – tg,n s /
– tg,n s /  < a <
< a < 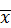 + tg,n s /
+ tg,n s /  ) = g. (3)
) = g. (3)
Здесь в скобках написано условие того, что значение неизвестного параметра a принадлежит некоторому промежутку, который и является доверительным интервалом. Его границы зависят от надежности g, а также от параметров выборки Его границы зависят от надежности g и параметров выборки 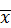 и s.
и s.
Чтобы определить значение tg по величине g, равенство (2) преобразуем к виду: P (|(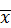 – a)
– a)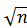 / s | ≥ tg,n) = 1 – g. Теперь по таблице для случайной величины t, распределенной по закону Стьюдента, по вероятности (1 – g) и числу степеней свободы (n – 1) находим tg,n. Формула (3) дает ответ на поставленную задачу.
/ s | ≥ tg,n) = 1 – g. Теперь по таблице для случайной величины t, распределенной по закону Стьюдента, по вероятности (1 – g) и числу степеней свободы (n – 1) находим tg,n. Формула (3) дает ответ на поставленную задачу.
Задача 2. На контрольных испытаниях 20-и электроламп средняя продолжительность их работы оказалась равной 2000 часов при среднем квадратическом отклонении, рассчитанном как корень квадратный из исправленной выборочной дисперсии, равном 11-и часам. Известно, что продолжительность работы лампы является нормально распределенной случайной величиной. Определить с надежностью 0,95 доверительный интервал для математического ожидания этой случайной величины.
Решение. Величина (1 – g)в данном случае равна 0,05. По таблице распределения Стьюдента при числе степеней свободы, равном 19, находим: tg,n = 2,093. Вычислим теперь точность оценки: 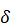 = 2,093´11 /
= 2,093´11 / 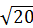 = 5,14. Отсюда получаем искомый доверительный интервал (1994,9; 2005,1).
= 5,14. Отсюда получаем искомый доверительный интервал (1994,9; 2005,1).
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 662; Нарушение авторских прав?; Мы поможем в написании вашей работы!