Вариационный ряд

Пусть для объектов генеральной совокупности определен некоторый признак или числовая характеристика, которую можно замерить (размер детали, удельное количество нитратов в дыне, шум работы двигателя). Эта характеристика — случайная величина x, принимающая на каждом объекте определенное числовое значение. Из выборки объема n получаем значения этой случайной величины в виде ряда из n чисел:

х ₁, х ₂,..., х _n.

Эти числа называются значениями признака. Среди чисел ряда могут быть одинаковые числа. Упорядочим значения признака в порядке возрастания, написав каждое значение лишь один раз, а затем под каждым значением х _i подпишем число m _i, показывающее сколько раз встречается данное значение, то получится таблица, называемая дискретным вариационным рядом:

х i	х 1	х 2	х 3	···	x n
m i	m 1	m 2	m 3	···	m k

Число m _i, называется частотой i -го значения признака. Очевидно, .

Если промежуток между наименьшим и наибольшим значениями признака в выборке разбить на несколько интервалов одинаковой длины, каждому интервалу поставить в соответствие число выборочных значений признака, попавших в этот интервал, то получим интервальный вариационный ряд. Если признак является непрерывной случайной величиной, то выборку приходится представлять именно таким рядом. Если в вариационном интервальном ряду каждый интервал заменить лежащим в его середине числом, 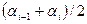, то получим дискретный вариационный ряд. Такая замена вполне естественна. Например, при измерении размера детали с точностью до одного миллиметра всем размерам из промежутка [49,5; 50,5) будет соответствовать одно число, равное 50.

Задача 1. В результате выборки получены числа

–3; 2; –1; –3; 5; –3; 2.

а) Для обработки выборки полезно построить точечную диаграмму. И её обязательно строят при обработке выборочных данных.

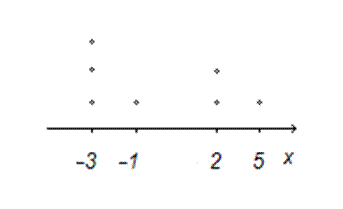Объём выборки равен n =7.

Теперь просто составить таблицу, которая и есть дискретный вариационный ряд.

х i	–3	–1
m i

б) Построим другую таблицу, удобную для дальнейших выкладок.

х i	–3	–1
m i/ n	3/7	1/7	2/7	1/7

в) Выпишем эмпирическую функцию распределения F *(х) аналогично тому, как строили функцию распределения для дискретных случайных величин.

Построим график эмпирической функции распределения F *(х):

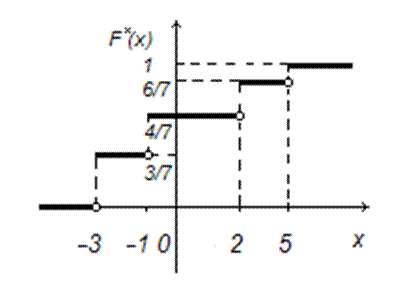
г) Построим полигон частот (или полигон относительных частот, если по оси у отложить m_i / n:

Задача 2. Построить гистограмму частот (или гистограмму относительных частот) по заданному дискретному вариационному ряду

х i	–2
m i

Решение.

Объём выборки равен n =33.

Разобьём весь промежуток [–2;7] на отрезки равной длины, например, на четыре

отрезка. Следовательно, длина каждого отрезка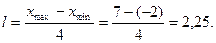

Высоту каждого прямоугольника выберем так, чтобы его площадь была равна числу

значений х _i, попавших в конкретный промежуток: h _j· l = m _j. Тогда 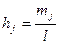. Следовательно, площадь такого многоугольника, который составлен из так построенных прямоугольников, равна объему выборки n. Результаты расчётов сведём в таблицу:

Интервал	[-2; 0,25)	[0,25; 2,5)	[2,5; 4,75)	[4,75; 7]
m j
h j		20/3	8/3	4/3

Теперь построим многоугольник, который называют гистограммой.

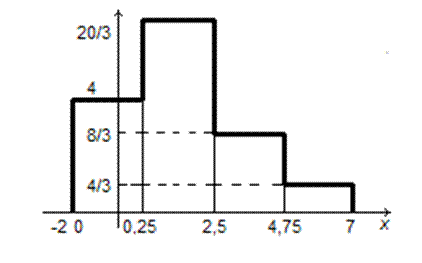От выбора длины отрезка l зависит большая или меньшая выразительность гистограммы.

Дата добавления: 2013-12-13