Точечные оценки параметров генеральной совокупности

Пусть выборка объема n представлена в виде вариационного ряда. Назовем выборочной средней величину

Величина 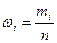— называется относительной частотой значения признака x _i. Естественно считать величину 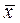выборочной оценкой параметра M ξ. Выборочная оценка параметра, представляющая собой число, называется точечной оценкой.

Выборочную дисперсию

.

можно считать точечной оценкой дисперсии D ξ генеральной совокупности.

Приведем еще один пример точечной оценки. Пусть каждый объект генера льной совокупности характеризуется двумя количественными признаками х и у. Например, в различных районах города измеряется концентрация вредных веществ в воздухе и фиксируется количество легочных заболеваний граждан в месяц. Или через равные промежутки времени сопоставляются доходность акций конкретной корпорации с каким-либо индексом, характеризующим среднюю доходность всего рынка акций. В этом случае генеральная совокупность представляет собой двумерную случайную величину (ξ, η). Эта случайная величина принимает значения (х, у) на множестве объектов генеральной совокупности. Не зная закона совместного распределения случайных величин ξ и η, нельзя говорить о наличии или тесноте корреляционной связи между ними, однако некоторые выводы можно сделать, используя выборочный метод.

Выборку объема n в этом случае представим в виде таблицы, где отобранный объект (i, j) представлен парой чисел (х _i, у _j), i =1,2,..., m; j =1,2,..., n.

y j x i	y1	y 2	…	y n
x 1	n 11	n 12	…	n 1n
x 2	n 21	n 22	…	n 2n
…	…	…	…	…
x m	n m1	n m2	…	n mn

Выборочный коэффициент корреляции рассчитывается по формуле

где ,

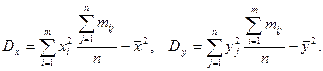
Выборочный коэффициент корреляции r _xy можно рассматривать как точечную оценку коэффициента корреляции ρ _ξη, характеризующего генеральную совокупность.

Дата добавления: 2013-12-13