Свойства несмещённости, состоятельности и эффективности точечных оценок

Точечные оценки являются случайными величинами, поскольку вычисляются по выборке и, естественно, различаются от выборки к выборке. Так какое же значение из них предпочесть?

Вводимые точечные оценки параметров должны удовлетворять трём свойствам: несмещённости, состоятельности и эффективности.

Пусть выборочный параметр δ рассматривается как выборочная оценка параметра θ генеральной совокупности. Если при этом выполняется равенство M δ =θ, то такая выборочная оценка называется несмещённой.

Можно доказать, что точечная оценка для математического ожидания генеральной совокупности удовлетворяет этому условию: 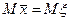. А точечная оценка D х для дисперсии нет. Поэтому её «поправляют» и вводится новая точечная оценка — исправленная выборочная дисперсия — 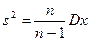, которая уже является несмещённой: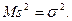

Полученная из выборки объема n точечная оценка δ _n параметра θ генеральной совокупности называется состоятельной, если она сходится по вероятности к θ. Это означает, что для любых положительных чисел ε и γ найдется такое число n _εγ, что для всех чисел n, удовлетворяющих неравенству n > n _εγ выполняется условие .

Доказательство и этого свойства выходит за рамки нашего курса.

Пусть имеется ряд несмещённых точечных оценок одного и того же параметра генеральной совокупности. Та оценка, которая имеет наименьшую дисперсию, называется эффективной.

Можно доказать, что для и s ² и Ds ² минимальны. Т.е. для точечной оценки, построенной по иному, дисперсия будет больше.

Таким образом, , s ² и r _xy являются несмещёнными, состоятельными и эффективными оценками величин М ξ, D ξ и ρ _ξη генеральной совокупности.

Задача 3. По выборке, приведённой в Задаче 1, вычислить и s ².

Решение приводится на доске.

Задача 4. Задана двумерная выборка (х₁,у₁), (х₂,у₂), …., извлечённая из двумерного распределения случайных величин (ξ, η). Чему равны 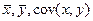и r _xy?

y j x i	─2

Решение приводится на доске.

Дата добавления: 2013-12-13