Вероятностное пространство.

Для построения законченной теории случайного эксперимента помимо введенных исходных понятий — случайного эксперимента, события, элементарного исхода, пространства элементарных исходов введем аксиому (пока для случая конечного или счетного пространства элементарных исходов).

Каждому элементарному исходу w_i пространства W соответствует некоторая неотрицательная числовая характеристика P_i шансов его появления, называемая вероятностью исхода w _i , причем

.

Суммирование ведется по всем i, для которых выполняется условие: w_i ÎW.

Отсюда следует, что 0 £ P_i £ 1 для всех i.

Вероятность любого событияА определяется как сумма вероятностей всех элементарных исходов, благоприятствующих событию А. Обозначим ее Р (А).

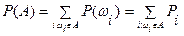(1)

Отсюда следует, что 1) 0 £ P (A) £ 1;

2) P (W)=1;

3) P (Æ)=0.

Будем говорить, что задано вероятностное пространство, если задано пространство элементарных исходов W и определено соответствие

w_i ® P (w_i ) =P_i.

Возникает вопрос: как определить из конкретных условий решаемой задачи вероятность P (w_i) отдельных элементарных исходов?

Классическое определение вероятности.

Вычислять вероятности P (w_i ) можно, используя априорный подход, который заключается в анализе специфических условий данного эксперимента до проведения самого эксперимента.

Возможна ситуация, когда пространство элементарных исходов состоит из конечного числа n элементарных исходов, причем случайный эксперимент таков, что вероятности осуществления каждого из этих n элементарных исходов представляются равными. Примеры таких случайных экспериментов: подбрасывание симметричной монеты, бросание правильной игральной кости, случайное извлечение игральной карты из перетасованной колоды. В силу введенной аксиомы вероятность каждого элементарного исхода в этом случае равна . Из этого следует, что если событие А содержит m элементарных исходов, то в соответствии с определением (1)

.

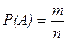В данном классе ситуаций вероятность события определяется как отношение числа благоприятных исходов к общему числу всех возможных исходов.

Пример 1. Из набора, содержащего десять одинаковых на вид электроламп, среди которых четыре бракованных, случайным образом выбирается пять ламп. Какова вероятность, что среди выбранных ламп будут две бракованные?

Прежде всего, отметим, что выбор любой пятерки ламп имеет одну и ту же вероятность. Всего существует способов составить такую пятерку, то есть случайный эксперимент в данном случае имеет равновероятных исходов.

Сколько из этих исходов удовлетворяют условию "в пятерке две бракованные лампы", т. е, сколько исходов принадлежат интересующему нас событию?

Каждую интересующую нас пятерку можно составить так: выбрать две бракованные лампы, что можно сделать числом способов, равным . Каждая пара бракованных ламп может встретиться столько раз, сколькими способами ее можно дополнить тремя небракованными лампами, то есть раз. Получается, что число пятерок, содержащих две бракованные лампы, равно ×.

Отсюда, обозначив искомую вероятность через P, получаем:

.

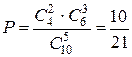Пример 2. Десять букв разрезной азбуки: А, А, А, Е, И, К, М, М, Т, Т произвольным образом выкладываются в ряд. Какова вероятность того, что получится слово МАТЕМАТИКА?

Решение приводится на доске.

Дата добавления: 2013-12-13