Дисперсия случайной величины

Определение. Дисперсия D xслучайной величины x — это математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

D x = M (x – M x)² =

Отметим, что и D x— математический оператор.

Выведем удобную для вычислений формулу дисперсии:

D x =

= .

Таким образом, дисперсия случайной величины равна разности математического ожидания квадрата случайной величины и квадрата её математического ожидания. Проще, дисперсия случайной величины равна «среднему квадрату минус квадрат среднего».

Задача 5. Рассмотрим случайную величину x с законом распределения

x
pi

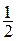
и вычислим её дисперсию.

Составим закон распределения случайной величины x²

x^2
pi

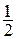
Вычислим M x²

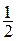M x² = 1× + 4× + 9× = .

Вычислим Mx

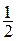M x = 1× + 2× + 3× = .

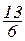Следовательно, D x =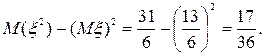

Дисперсия характеризует степень рассеяния значений случайной величины относительно её математического ожидания. Если все значения случайной величины тесно сконцентрированы около её математического ожидания и большие отклонения от математического ожидания маловероятны, то такая случайная величина имеет малую дисперсию. Если значения случайной величины рассеяны и велика вероятность больших отклонений от математического ожидания, то такая случайная величина имеет большую дисперсию.

Дисперсия случайной величины всегда неотрицательна и равна нулю в том и только в том случае, когда эта случайная величина – константа.

Свойства дисперсии.

1. Если с – число, то D (x + с) = D (x).

2. Если k – число, то D (k x) = k ² D x. Докажем

D (k x) = M (k x – M (k x))² = M (k x – k M x)² = M (k ² (x – M x)²) = k ² M (x – M x)² = k ² D x.

3. Для двух независимых случайных величин x и h справедливо равенство

D( x + h) = D x + D h.

Это свойство проверим на примере.

Задача 6. Пусть x и h – независимые случайные величины с заданными законами распределения:

x				h
pi	1/4	3/4		pi	7/10	3/10

Покажем, что D( x + h ) = D x + D h.

Вычислим дисперсии x и h по ранее изложенному алгоритму:

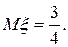
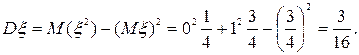
Следовательно, D x + D h = 3/16 + 21/100 = 159/400.

Построим закон распределения для случайной величины x + h:

x + h
pi	1/4·7/10 = 7/40	1/4·3/10 = 3/40	3/4·7/10= 21/40	3/4·3/10 = 9/40

x + h
pi	7/40	24/40	9/40

( x + h ) ^2
pi	7/40	24/40	9/40

M( x + h ) ² = 184/40, M (x + h ) = 82/40. Следовательно, D (x + h ) = 23/5 - (41/20)² = 159/400.

Отметим, дисперсия даёт несколько искажённое представление о самой величине отклонений, измеряя их в квадратных единицах.

Дата добавления: 2013-12-13