Общие физические понятия процессов преобразования энергии

Параметры механической системы

Масса М - характеристика элемента, обладающего инерцией; такой пассивный элемент, который накапливает кинетическую энергию движения.

Пружины характеризуются жесткостью К; это пассивные элементы, накапливающие потенциальную энергию.

Демпферы определяют вязкое трение, преобразуя кинетическую энергию в тепло.

Во вращающихся системах определяют источники момента и угловой скорости, а в качестве параметров соответственно - полярный момент инерции; крутильная жесткость К и сопротивление вращению (крутильное сопротивление).

Как и элементы электрических цепей, механические элементы - математические абстракции. Реальные элементы обладают одновременно несколькими свойствами, приписываемыми идеализированным элементам.

Обозначения:

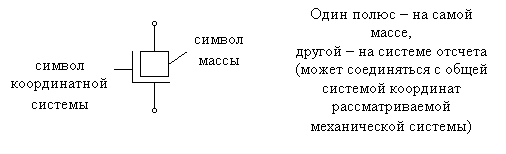
Масса М

Пружина К

Демпфирующий элемент

Есть, нужно полагать, в преобразователе еще нечто, связывающее электрическую и механическую системы и определяющее преобразование одного вида энергии в другой.

Это нечто - поле. Электрическое или магнитное. С ним и связаны неприятности и сложности анализа процессов в преобразователе.

Имея дело с механической системой, мы говорим о механических узлах и механических контурах.

Далее. Анализируя процессы преобразования энергии в электрических цепях, мы говорим о поступлении энергии в цепи через электрические зажимы или систему электрических зажимов. Можно сделать шаг в направлении объединения понятий (универсализации!), определяющих электрические и механические цепи.

Давайте скажем, что механическая система имеет свои "зажимы" - механические, через которые в нее извне поступает механическая мощность (энергия).

Наши рассуждения связаны с тем, что изучаемые устройства - электромеханические преобразователи энергии - представляют системную совокупность двух составляющих: электрической и механической. И та, и другая, в соответствии с нашими представлениями, имеет зажимы. Если энергия поступает в преобразователь из электрических сетей через электрические зажимы, то она преобразуется в механическую энергию, которая снимается с механических зажимов. Если же энергия поступает на механические зажимы, то она преобразуется в электрическую и отдается во внешние сети.

Таким образом электромеханический преобразователь преобразует потоки энергии, поступающие в него от внешних источников.

Преобразование энергии здесь осуществляется за счет особого состояния среды внутри устройства, которое называется полем.

Очевидно, что при создании и использовании преобразователя необходимо позаботиться о создании этой среды - поля.

Поле должно иметь требуемые (известные) количественные и качественные характеристики.

Электромеханический преобразователь обладает замечательным свойством - он обратим.

То есть, любой электромеханический преобразователь может работать и в режиме двигателя, преобразуя электрическую мощность сетей в механическую мощность на валу, и в режиме генератора, преобразуя механическую мощность, подводимую к валу, в электрическую мощность, отдаваемую сетям.

Введение понятия "мощность на валу" определяет то, что в дальнейшем наше внимание будет сосредоточено на вращающихся электромеханических преобразователях. Хотя, справедливости ради, необходимо сказать, что есть значительный класс преобразователей, совершающих поступательное движение.

Основной характеристикой преобразователя является характеристика "вход-выход", которая представляется соответствующими дифференциальными уравнениями.

При изучении процессов преобразования энергии основное внимание следует обратить на электромагнитный процесс, определяющий переход электрической энергии в механическую и механической в электрическую.

В практике преимущественно используются магнитные устройства, то есть устройства, "работающие от тока" (ток - источник магнитного поля!). Причина преимущества следует из сравнения выражений для плотности энергии электрического и магнитного полей

и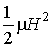

где e имеет порядок 10^-11 Ф/м, а m - 10^-6 Гн/м.

Основной характеристикой любого преобразователя энергии является механическая характеристика, связывающая механическую силу с движением. Здесь мера движения - пройденный путь S, либо скорость n.

Естественно установление связи силы и движения (они характеризуют механическую часть системы!) с напряжениями U и токами i сетей и цепей преобразователя (электрическая часть преобразователя!). И эту связь устанавливает магнитное поле в соответствии с принципами М. Фарадея и А. Ампера!

1. Закон М. Фарадея (закон электромагнитной индукции) в точном соотношении имеет вид:

,

(2.1)

где 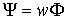- потокосцепление.

Это уравнение определяет, что величина ЭДС пропорциональна скорости изменения во времени потока Ф, связанного с цепью (с числом витков w). Знак минус учитывает направление индуцируемой ЭДС в соответствии с законом Ленца.

2. На проводник с током в магнитном поле действует механическая сила f_m. Механическая сила возникает и в том случае, если в магнитное поле поместить железо.

Электромеханический преобразователь, принцип действия которого основан на законе электромагнитной индукции, конструктивно является совокупностью катушек с железными сердечниками. Пример исполнения преобразователя в поперечном сечении приведен на рис. 2.1.

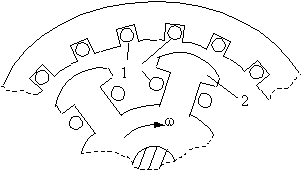
Рис. 2.1. Поперечное сечение преобразователя.

1 - проводники катушек; 2 - сердечники

Ток, протекающий в катушках, создает магнитное поле. Сердечники, обладающие высокой магнитной проницаемостью m, канализируют (направляют) поток Ф вектора магнитной индукции 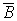. Таким образом, при анализе процессов в преобразователе, наряду с электрической и механической цепями, необходимо, в общем случае, рассматривать еще и магнитную цепь.

Процессы в магнитной цепи электромеханического преобразователя обусловлены неприятной особенностью основной характеристики ферромагнитных материалов - характеристики намагничивания (рис. 2.2); она нелинейна.

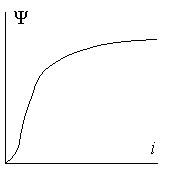
Рис. 2.2. Характеристика намагничивания электротехнического железа

При изучении основных свойств электромеханических преобразователей с целью упрощения анализа нелинейную зависимость Y = Y(i) с известной точностью заменяют линейной (рис. 2.3).

Рис. 2.3. Замена Y = Y(i) линейной функцией

Проведенная замена позволяет установить постоянный коэффициент связи между током i и потокосцеплениемY. Это - индуктивность

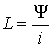
(2.2)

Исходными уравнениями при анализе процессов в электромеханических преобразователях являются известные уравнения Максвелла:

,

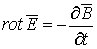(2.3)

,

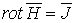(2.4)

где 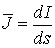- вектор плотности токов в катушках, А/м².

Уравнения (2.3) и (2.4) здесь записаны в виде, соответствующем сравнительно низким частотам, характерным большинству электромеханических преобразователей.

В предельных переходах уравнение (2.3) дает известное уравнение Максвелла для контура k:

,

где U_k - напряжение на зажимах контура,
i_kR_k - падение напряжения на активном сопротивлении R_k контура,
e_k = -dY_k/dt - ЭДС, наведенная в контуре изменяющимся потокосцеплением,

а уравнение (2.4) - уравнение для i-й ветви магнитной цепи:

,

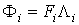(2.6)

где 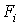- магнитодвижущая сила (МДС) i-й ветви магнитной цепи;
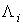- магнитная проводимость i-й ветви.

Уравнение (2.6) - закон Ома для участка магнитной цепи.

При подстановке в (2.6) МДС получим . Умножим правую и левую части на w:

,

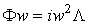или

.

И индуктивность

.

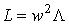Дата добавления: 2013-12-13