
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
К началу К следующей лекции
|
|
|
|
Таблица 3.1
2. 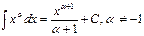
| 9. 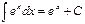
|
2. 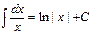
| 10. 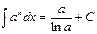
|
3. 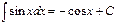
| 12. 
|
4. 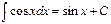
| 12. 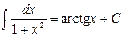
|
5. 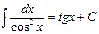
| 13. 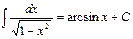
|
6. 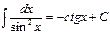
| 14. 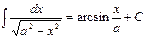
|
7. 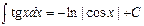
| 15. 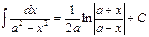
|
8. 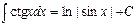
| 16. 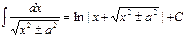
|
В силу определения (3.2) отыскание неопределенного интеграла сводится к нахождению одной из первообразных подынтегральной функции f(x). Поскольку 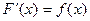 , то интегрирование является операцией обратной дифференцированию.
, то интегрирование является операцией обратной дифференцированию.
Чтобы проверить правильно ли выполнено интегрирование необходимо продифференцировать результаты и получить подынтегральную функцию.
Согласно (3.2) имеем:
а) 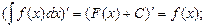
б) 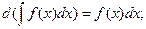
в) 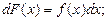
г) 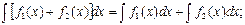 (3.3)
(3.3)
д) 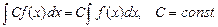 . (3.4)
. (3.4)
Справедливость свойств интегралов г) и д) и следующих равенств проверяется дифференцированием обеих частей:
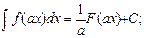 (3.5)
(3.5)
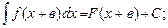 (3.6)
(3.6)
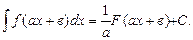 (3.7)
(3.7)
Пример 1. Найти 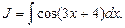
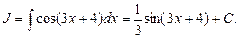 Здесь использовали формулу (3.7) и табличный интеграл 4 (см. табл. 3.1).
Здесь использовали формулу (3.7) и табличный интеграл 4 (см. табл. 3.1).
Пример 2. Найти 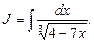
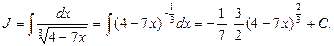
3.3. Основные методы интегрирования
1. Метод разложения
Используя свойства подынтегральной функции, преобразуем ее к виду
f (x) = af 1(x) + bf2 (x)
и представим искомый интеграл на основании формул (3.3) и (3.4) в виде суммы более простых, желательно табличных интегралов:
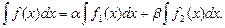
Пример 3. Найти 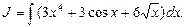
Подынтегральная функция уже представлена в виде суммы трех слагаемых, поэтому используя формулы (3.3) и (3.4), получим:
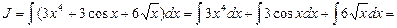
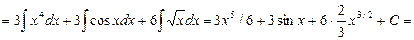
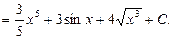
Пример 4. Найти 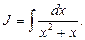
Представим подынтегральную функцию в виде суммы слагаемых:
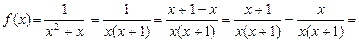
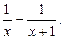
Тогда 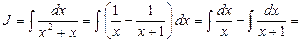
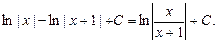
Искомый интеграл удалось разложить на сумму двух табличных интегралов.
Пример 5. Найти 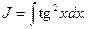
Так как 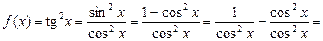
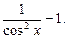 Тогда
Тогда 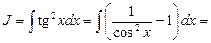
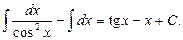
Пример 6. Найти 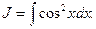
Для преобразования подынтегральной функции f(x) воспользуемся тригонометрической формулой понижения степени:
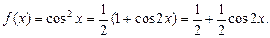
Тогда 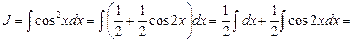

2. Метод замены переменной
Этот метод позволяет заменить переменную в неопределенном интеграле с помощью подстановок двух видов.
Первый вариант подстановки. Если x = j(t) непрерывна вместе со своей производной, то справедливо равенство
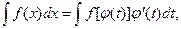 (3.8)
(3.8)
называемое формулой замены переменной. Как и всякое интегральное равенство, оно проверяется дифференцированием обеих частей.
Функция x = j(t) выбирается из соображений упрощения искомого интеграла. После интегрирования необходимо вернуться к старой переменной подстановкой 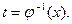
Пример 7. Найти 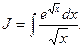
Воспользуемся методом замены переменной, чтобы освободиться от иррациональности:
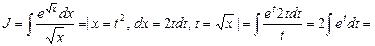
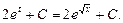
Найдя интеграл от новой переменной t, необходимо затем вернуться к старой переменной х.
Второй вариант подстановки. В большинстве случаев целесообразно за новую переменную t принять некоторую функцию от х, т.е. 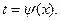 Формула замены переменной в этом случае имеет вид:
Формула замены переменной в этом случае имеет вид:
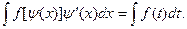 (3.8¢)
(3.8¢)
Пример 8. Найти 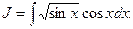
Чтобы произвести замену переменной, воспользуемся формулой (3.8¢):
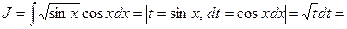
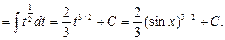
Подстановка 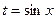 выбрана удачно, так как с ее помощью искомый интеграл привели к табличному (см. табл. 3.2. п. 1).
выбрана удачно, так как с ее помощью искомый интеграл привели к табличному (см. табл. 3.2. п. 1).
Пример 9. Найти 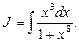
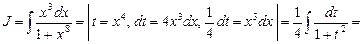
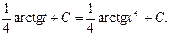
При выборе удачной подстановки, сводящей искомый интеграл к табличному, полезно обратить внимание на следующие соотношения, позволяющие подвести множитель под знак дифференциала.
Например, учитывая, что 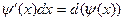 , найдем:
, найдем:
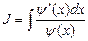 =
= 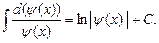
В таком случае можно и не вводить явное обозначение новой переменной. Полезной для нахождения многих интегралов является приводимая ниже табл. 3.2.
Таблица 3.2
2. 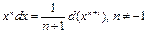
| 7. 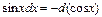
|
2. 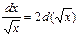
| 8. 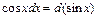
|
3. 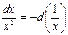
| 9. 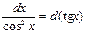
|
4. 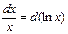
| 10. 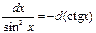
|
5.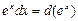
| 12. 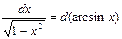
|
6. 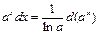
| 12. 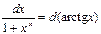
|
Так, в примере 9, учитывая, что 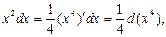 искомый интеграл примет вид:
искомый интеграл примет вид:
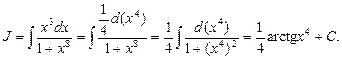
Здесь х 4 приняли за новую переменную без обозначения ее буквой t. Необходимость возвращаться к старой переменной отпадает.
Пример 10. Найти 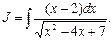
Заметим, что 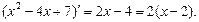 Теперь выделим в числителе производную знаменателя:
Теперь выделим в числителе производную знаменателя:
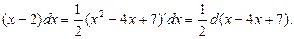
Таким образом, 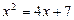 можно принять за новую переменную.
можно принять за новую переменную.
Тогда 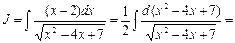
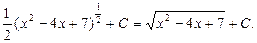
Пример 11. Найти 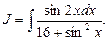
Заметим, что 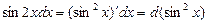 и sin2 x можно принять за новую переменную.
и sin2 x можно принять за новую переменную.
Тогда: 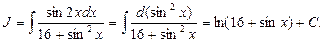
При решении дополнительно воспользовались формулой (3.6).
Замечание. В большинстве случаев при отыскании неопределенных интегралов можно применять сочетание методов разложения и подстановки (замены переменной).
Пример 12. Найти 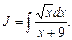
Сначала воспользуемся методом замены переменной:
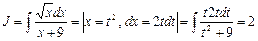
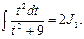
Для отыскания интеграла J 1 используем теперь метод разложения:
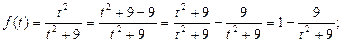
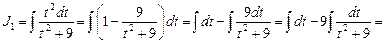
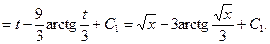
Окончательно получим:
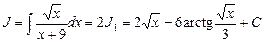 , где С = 2 С 2.
, где С = 2 С 2.
Пример 13. Найти 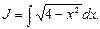
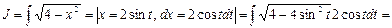
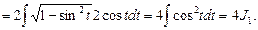
Воспользуемся результатом примера 6:
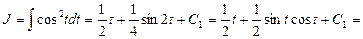
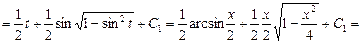
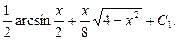
Окончательно получим:
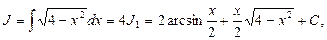 где С = 4 С 2.
где С = 4 С 2.
Пример 14. 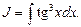 .
.
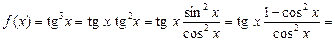
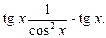
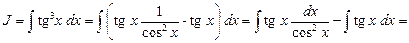
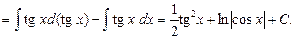
Пример 15. Найти 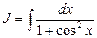 .
.
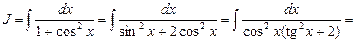
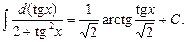
Пример 16. Найти 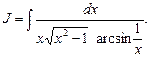
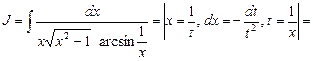
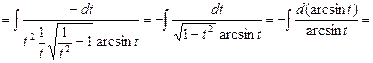
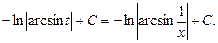
3. Метод интегрирования по частям
Интегрируя выражение 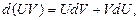 получим:
получим: 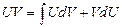 или
или 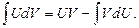
Эта формула интегрирования по частям. Здесь U(x) и V(x) – дифференцируемые функции х.
Выражение f(x)dx необходимо так разбить на сомножители U и dV, чтобы нахождение V и интеграла 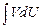 было проще, чем вычисление исходного интеграла.
было проще, чем вычисление исходного интеграла.
В случае интегралов вида
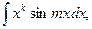
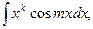
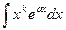
берем 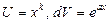 или
или 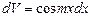 или
или 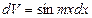 ,
,
а для интегралов
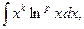
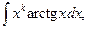
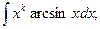
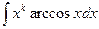
берем 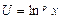 или
или 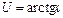 или
или 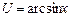 или
или 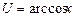 , а
, а 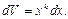
Пример 17. Найти 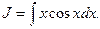
Применим метод интегрирования по частям. U и dV берем согласно рекомендациям:
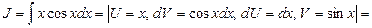
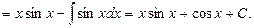
Пример 18. Найти 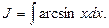
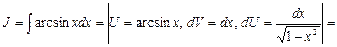
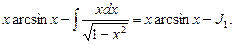
Найдем интеграл J 1 методом замены переменной. Учитывая, что 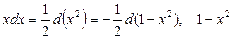 примем за новую переменную.
примем за новую переменную.
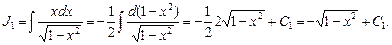
Окончательно получим:
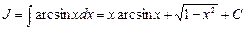 , где С = - С 2.
, где С = - С 2.
Пример 19. Найти 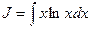
В этом случае за U следует обозначить ln x.
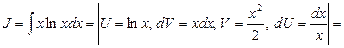
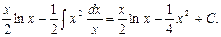
В некоторых случаях при интегрировании по частям можно и не вводить явно U и V.
Например,
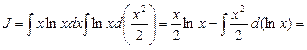
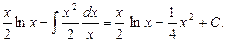
Пример 20. Найти 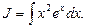
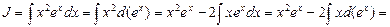
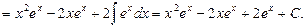
В этом случае формула (2.9) интегрирования по частям применяется дважды.
Пример 21. Найти 
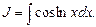
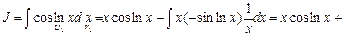
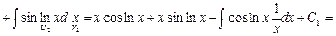
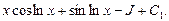
Таким образом, получили уравнение относительно неизвестного интеграла J. Искомый интеграл найдем, решив это уравнение: 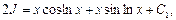 откуда получим:
откуда получим:
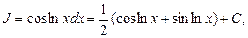 где
где 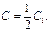
Аналогично вычисляются: 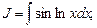
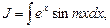
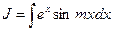 .
.
Анализ этих примеров показывает, что интегрирование по частям состоит из следующих шагов:
1) разбиение f(x)dx на U и dV;
2) нахождение V и dU;
3) применение формулы (2.9);
4) нахождение 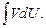
При необходимости интегрирование по частям выполняется неоднократно.
Например, для 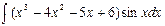 оно выполняется три раза. Этот пример решить самостоятельно.
оно выполняется три раза. Этот пример решить самостоятельно.
3.4. Интегрирование рациональных функций
Рациональная дробь 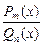 называется правильной, если m < n, т.е. степень n многочлена Qn(x) больше, чем степень m многочлена Pm(x). При
называется правильной, если m < n, т.е. степень n многочлена Qn(x) больше, чем степень m многочлена Pm(x). При 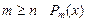 делим на Qn(x) по правилу деления многочленов и представляем рациональную дробь как сумму многочлена и правильной дроби.
делим на Qn(x) по правилу деления многочленов и представляем рациональную дробь как сумму многочлена и правильной дроби.
Дроби вида 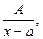
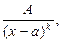
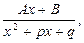
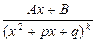 называются простейшими. Здесь
называются простейшими. Здесь 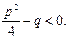
Простейшие дроби интегрируются следующим образом:
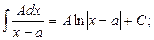
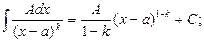
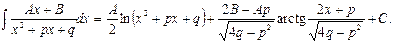
Пример 22. 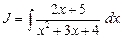
Выделим в числителе производную знаменателя:
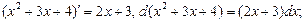
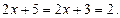
Тогда получим:
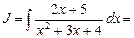
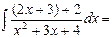
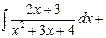
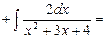
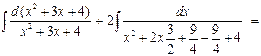
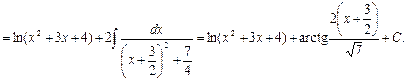
Правильные рациональные дроби интегрируются разложением на сумму простейших дробей.
Вид разложения правильной дроби на простейшие зависит от типов множителей, входящих в разложение многочлена Q(x) на множители, а именно:
1) каждому линейному множителю х-а отвечает дробь 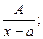
2) каждому линейному множителю х-а кратности k отвечает сумма дробей:
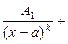
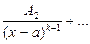 +
+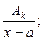
3) каждому квадратичному множителю 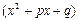 отвечает слагаемое:
отвечает слагаемое:
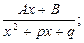
4) каждому квадратичному множителю 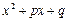 кратности k отвечает сумма дробей:
кратности k отвечает сумма дробей:
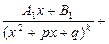
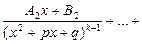
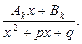
Пример 23. Найти 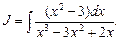
Разложим многочлен 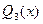 на линейные и квадратичные множители:
на линейные и квадратичные множители:
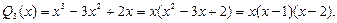
Пользуясь рекомендациями, разложим подынтегральную функцию на сумму простейших дробей:
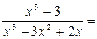
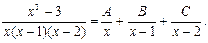 (3.10)
(3.10)
Определим неизвестные коэффициенты А, В и С, используя так называемый метод неопределенных коэффициентов. Для этого приводим дроби в равенстве (3.10) к общему знаменателю. Затем, чтобы освободиться от знаменателей, умножим обе части равенства на 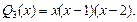
В результате получим:
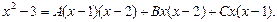 (3.11)
(3.11)
Два многочлена тождественно равны в случае, если коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества равны.
В нашем случае: 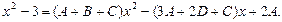
Приравняв коэффициенты при одинаковых степенях х, получим систему линейных уравнений:
| х 2 | А | + | В | + | С | = | |
| х 1 | 3А | + | 2В | + | С | = | |
| х 0 | 2А | = | -3. |
Решив эту систему, найдем: 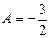 , В = 2,
, В = 2, 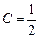 .
.
Тогда разложение подынтегральной дроби на простейшие примет вид:
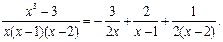
Таким образом,
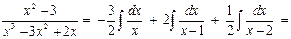
Замечание 2. В случае простых корней знаменателя дроби 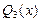 неизвестные коэффициенты находятся особенно легко – подстановкой в тождество (2.11) в качестве частных значений многочленов этих корней: х 1 = 0, х 2 = 1 и х 3 = 2:
неизвестные коэффициенты находятся особенно легко – подстановкой в тождество (2.11) в качестве частных значений многочленов этих корней: х 1 = 0, х 2 = 1 и х 3 = 2:
| х 1 = 0 | -3 = 2А, | А = 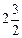
|
| х 2 = 1 | -2 = -В, | В = 2 |
| х 3 = 2 | 1 = 2С, | С = 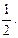
|
Замечание 2. Возможно и сочетание обоих методов (метода сравнения коэффициентов и метода частных значений).
Пример 24. Найти 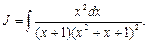
Подынтегральная функция может быть разложена на сумму простейших дробей:
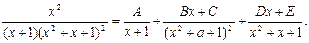
Отсюда имеем: 
Подставим в тождество сначала частные значения. Так х = -1 является простым корнем знаменателя:
| х = -1 | 1 = А |
| х = 0 | 0 = А + С + Е, откуда С + Е = -2. |
Теперь приравняем в тождестве коэффициенты при одинаковых степенях х:
| х 4 | 0 = А + D, откуда D = -1 |
| х 3 | 0 = 2 А + 2 D + Е, откуда E = 0, тогда С = -1 |
| х 2 | 1 + 3 А + 2 D + 2 E + B, откуда В = 0. |
Следовательно,
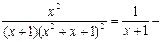
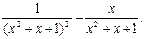
Тогда: 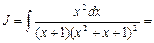
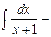
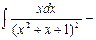
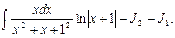
Найдем сначала интеграл 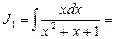
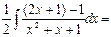
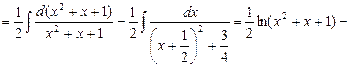
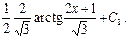
Для отыскания интеграла J 2 используем рекуррентную формулу:
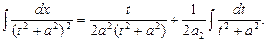
Тогда:
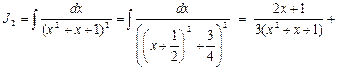
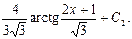
Здесь выполнена подстановка 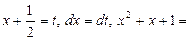
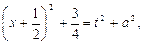 где
где 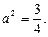
Окончательно получим:
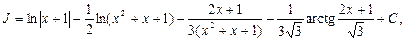 где
где 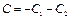 .
.
Приведем схему разложения правильной рациональной дроби на сумму простейших дробей:
1) разложить знаменатель дроби 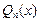 на линейные и квадратичные множители;
на линейные и квадратичные множители;
2) разложить подынтегральную дробь на сумму простейших дробей, но с неопределенными коэффициентами (тип простейшей дроби зависит от множителя, входящего в знаменатель);
3) для отыскания неопределенных коэффициентов привести полученное равенство к общему знаменателю, затем освободиться от знаменателей;
4) составить систему линейных уравнений относительно неизвестных коэффициентов и решить ее;
5) найденные коэффициенты подставить в разложение подынтегральной дроби на сумму простейших дробей.
Пример 25. Найти 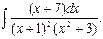
Подынтегральная функция является правильной рациональной дробью, и она может быть представлена в виде суммы простейших дробей:
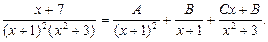
Отсюда 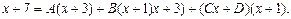
Неизвестные коэффициенты А, В, С найдем из системы:
| х 3 | 0 = В + С |
| х 2 | 0 = А + В + D + 2 C |
| x 1 | 1 = 3 B + C + 2 D |
| x 0 | 7 = 3 A + 3 В + 3 D. |
Решив эту систему, найдем 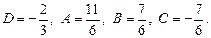
Искомое разложение примет вид:
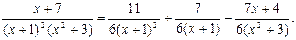
Таким образом, 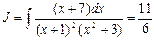
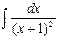 +
+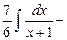
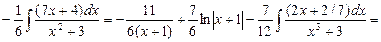
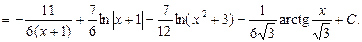
В некоторых случаях удается проинтегрировать рациональную дробь, не разлагая ее на сумму простейших дробей, а более простым способом.
Например, для 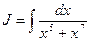 подынтегральную функцию можно разложить на сумму простейших дробей. Так как
подынтегральную функцию можно разложить на сумму простейших дробей. Так как 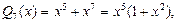 то имеем разложение:
то имеем разложение:
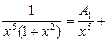
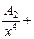
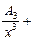
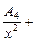
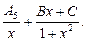
Такое разложение нецелесообразно, так как для нахождения неизвестных коэффициентов придется составить и решить систему 7-ми линейных уравнений с 7-ю неизвестными, что приведет к громоздким вычислениям.
Разложить подынтегральную функцию на интегрируемые слагаемые можно и другим способом:
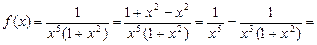
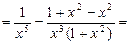
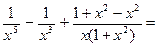
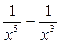
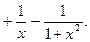
Тогда искомый интеграл примет вид:
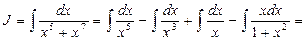
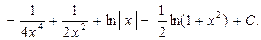
В последнем интеграле, учитывая, что 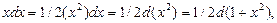
за новую переменную приняли 1 + х 2.
3.5. Интегрирование иррациональных функций
1. Интегралы вида 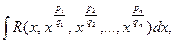 где R – рациональная функция своих аргументов, приводятся к интегралам от рациональных дробей подстановкой
где R – рациональная функция своих аргументов, приводятся к интегралам от рациональных дробей подстановкой 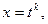 где k – наименьшее общее кратное чисел
где k – наименьшее общее кратное чисел 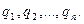
2. Интегралы вида 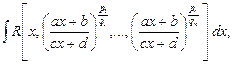
где R – рациональная функция своих аргументов, приводятся к интегралам от рациональных дробей подстановкой 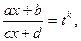 где k – наименьшее общее кратное чисел
где k – наименьшее общее кратное чисел 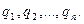
3. С помощью тригонометрических подстановок можно находить интегралы:
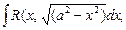
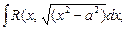
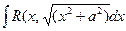
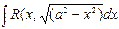 находится подстановкой
находится подстановкой 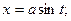
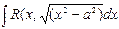 находится подстановкой
находится подстановкой 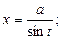
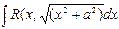 находится подстановкой
находится подстановкой 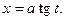
Пример 26. Найти 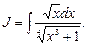
Здесь 
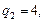 поэтому k = 4. Искомый интеграл находим с помощью подстановки
поэтому k = 4. Искомый интеграл находим с помощью подстановки 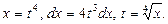
Тогда:
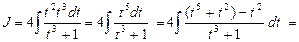
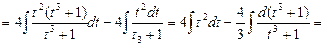
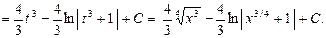
3.6. Интегрирование тригонометрических функций
Интегралы вида 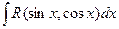 с помощью универсальной тригонометрической подстановки
с помощью универсальной тригонометрической подстановки 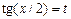 сводятся к интегралам от рациональных функций.
сводятся к интегралам от рациональных функций.
Пусть 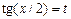 . Тогда имеем
. Тогда имеем 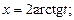
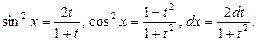
Здесь 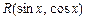 - рациональная функция от sin x и cos x.
- рациональная функция от sin x и cos x.
Пример 27. Найти 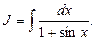
Применим универсальную тригонометрическую подстановку 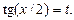
Тогда получим:
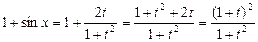 и
и 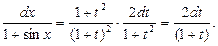
Искомый интеграл примет вид:
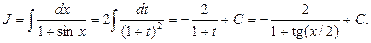
Подстановка 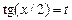 часто приводит к сложным выражениям, и поэтому в зависимости от вида функции
часто приводит к сложным выражениям, и поэтому в зависимости от вида функции 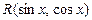 применяются другие подстановки:
применяются другие подстановки:
1) 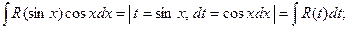
2) 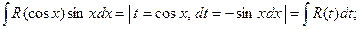
3) 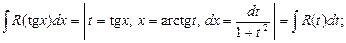
4) если sin x и cos x входят только в четных степенях, по применяется подстановка 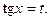
При этом 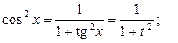
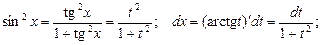
5) 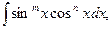 где m и n – целые числа.
где m и n – целые числа.
Если 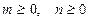 и оба числа четные, то применяются тригонометрические формулы понижения степени, упрощающие исходный интеграл:
и оба числа четные, то применяются тригонометрические формулы понижения степени, упрощающие исходный интеграл:
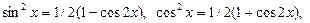
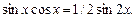
Если, по крайней мере, одно из чисел нечетное, то имеем случай 1) или 2).
Если оба числа четные и хотя бы одно из них отрицательное, то следует делать замену 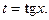
Пример 28. Найти 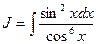 .
.
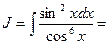
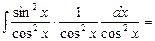
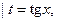
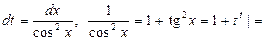
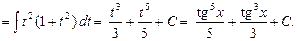
Пример 29. Найти 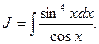
В этом примере n = -1 – нечетное. Поэтому используем подстановку 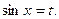 Тогда
Тогда 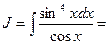
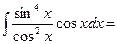
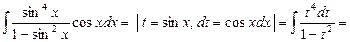
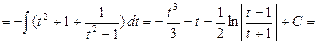
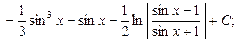
6) интегралы 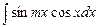 ,
, 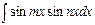 ,
, 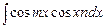 находятся с помощью преобразования произведения в сумму или разность:
находятся с помощью преобразования произведения в сумму или разность:
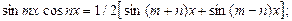
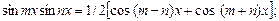
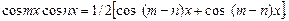
Пример 30. Найти 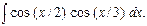
Преобразуем произведение тригонометрических функций в сумму, используя последнюю формулу:
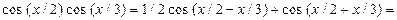
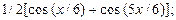
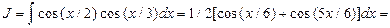
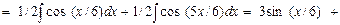
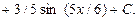
 Пример 31. Найти
Пример 31. Найти 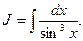
Разложим подынтегральную функцию на сумму интегрируемых слагаемых:
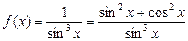
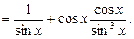
Тогда получим:
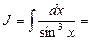
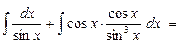
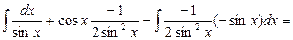
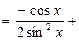
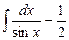
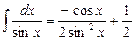
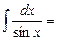
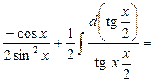
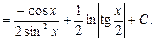
Здесь использовали в первом интеграле, что
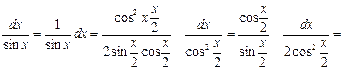
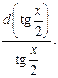
При отыскании второго интеграла использовали метод интегрирования по частям:
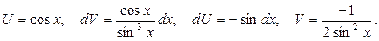
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 491; Нарушение авторских прав?; Мы поможем в написании вашей работы!