Атаки, не зависящие от уязвимостей алгоритма

Криптостойкость криптографических хэш-функций

На криптографические хэш-функции возможны следующие атаки:

1. Нахождение прообраза М по заданному значению Н_М= h(М).

Такая атака особенно опасна для систем аутентификации, использующих хэш-образы паролей и секретных ключей;

2. Нахождение второго прообраза М’ по заданному прообразу М, для которого выполняется условие h(M) = h(M’).

Эта атака может быть использована для фальсификации сообщения при контроле целостности с использованием хэш-функции (Пример).

3. Нахождение коллизии,т.е. двух прообразов М и М’,, для которых выполнялось бы условие h(M) = h(M’).

Эта атака может быть использована для фальсификации сообщения, подписанного цифровой подписью (Пример).

При использовании вероятностной атаки для нахождения прообраза (второго прообраза) вероятность нахождения второго прообраза (вероятность успеха атаки навязывания) Рн можно оценить по формуле

Рн = 1/2^LА

Так как хэш-функция не содержит секретных параметров, то наряду с вероятностной атакой возможны и детерминированные.

Все детерминированные атаки на хэш-функции можно разделить на две группы: атаки, базирующиеся на уязвимости конкретного алгоритма преобразований (аналитические) и атаки, не зависящие от уязвимостей алгоритма.

1. Атака “грубой силой” может быть использована при нахождения прообраза по заданному хэш-образу. Суть атаки заключается в последовательном или случайном переборе входных сообщений и сравнения полученного хэш-образа с заданным. Сложность такой атаки оценивается 2^L-1 операций вычисления хэш-образа, где L - длина хэш-образа в битах.

Обоснование.

Криптоаналитик формирует некоторое число произвольных сообщений М₁,М₂, …, М_к, вычислят их хэш-образы Н_М1, Н_М2, …, Н_Мк и сравнивает их значения с заданным Н_М1. Атака окажется успешной, если будет найдена хотя бы одна коллизия. Вероятность нахождения второго прообраза (вероятность успеха атаки навязывания) Р_К можно оценить по формуле

Р_К = 1- (1- 1/2^LА)^К

где

К - число вычисленных хэш-образов;

LА = || Н_М || - длина хэш-образа.

Сложность атаки навязывания (количество испытаний К, при котором Р_К =0.5)

К > 2^LА-1.

Пример – см. Таблицу 3.1.

2. Атака методом “дня рождения” выполняется для нахождения коллизии, то есть двух различных сообщений с одинаковыми хэш-образами. Эта атака основана на известном в теории вероятности парадоксе “дня рождения”* и заключается в том, что в двух сгенерированных множествах хэш-образов, содержащих 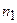и 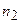элементов соответственно, вероятность нахождения коллизии оценивается следующей формулой:

Рн ≈ еxp(–n₁n₂/2^LА )

В частности, при 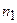= = 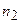2 ^{0.5 L}

сложность атаки К (число вычислений хэш-образа)

К=2^LА/2+1,

а вероятность нахождения коллизии

Р_К ≈ 1 – 1/e ≈ 0.63

Так как на современном уровне минимальная сложность атаки должна быть не меньше, чем 2¹²⁸ , то длина хэш-образа L для обеспечения стойкости к атаке нахождения коллизии методом «дня рождения» должна быть не менее 256 бит, т.е. в два раза больше, чем для обеспечения стойкости к атаке нахождения второго прообраза.

* Парадоксе “дня рождения”

· Парадокс “дня рождения” является стандартной статистической проблемой.

· А) Сколько человек должно собраться, чтобы с вероятностью равной 0.5 хотя бы у одного из них был общий с Вами день рождения? Ответ: 183

· В) Сколько человек должно собраться, чтобы с вероятностью равной 0.5 хотя бы у двоих из них был общий день рождения? Ответ: 23

Таблица 3.1 Характеристики криптостойкости хэш-функций

Длина хэш-образа LА, бит	Нахождение второго прообраза
Вероятностная атака   Рн	Детерминированная атака (Рн =0.5) Время (MIPS-лет)	Детерминированная атака (Рн =0.5) Время (MIPS-лет)
	1,08 × 10^–19	3×10^5	1,19 часа
	5,88 × 10^–39	5,4 × 10^24	6×10^5
	1,73 × 10^–77	1,8 × 10^63	1,1 × 10^25
	1,49 × 10^–154	2,1 × 10^140	3,7 × 10^63

Одна MIPS (Million Instruction Per Second) машина хэширует миллион сообщений в секунду. При таких условиях число хэш-образов, вычисленных одной MIPS машиной за один год составляет 3.15×10¹³.

Дата добавления: 2013-12-13