Кинематическое исследование пространственных планетарных механизмов методом планов угловых скоростей

Графическое определение передаточного отношения.

Аналитическое определение передаточного отношения.

Двухрядный механизм с двумя внутренними зацеплениями.

Графическое определение передаточного отношения.

Рис.15.7

В планетарном редукторе, изображенном на рис.15.6 на звене 2 нарезаны два зубчатых венца:

z2, который зацепляется с зубчатым венцом z1 звена 1

z3, который зацепляется с внутренним зубчатым венцом z4 звена 3.

По формуле Виллиса отношение угловых скоростей звеньев для внутреннего зацепления колес z2 и z1:

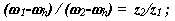
для внутреннего зацепления колес z4 и z3:

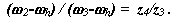
Перемножим, правые и левые части этих уравнений, и получим:

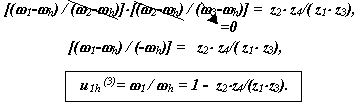
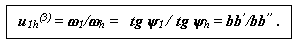
Рассмотрим этот метод исследования на примере планетарного механизма конического дифференциала заднего моста автомобиля. На рис. 15.8 изображена схема механизма и планы угловых скоростей.

Рис.15.8

Планы угловых скоростей строятся в соответствии с векторными уравнениями:

w2=w1+w21; w4=w3+w43

w3=w2+w32; w5=w3+w53

Вектора относительных угловых скоростей направлены по осям мгновенного относительного вращения:

w21 - по линии контакта начальных конусов звеньев 2 и 1;
w32 - по оси шарнира С;
w43 - по линии контакта начальных конусов звеньев 4 и 3;
w53 - по линии контакта начальных конусов звеньев 5 и 3.

Вектора абсолютных угловых скоростей направлены по осям кинематических пар, которые образуют звенья со стойкой:

w2 - по оси пары В; w1 - по оси пары А;
w4 - по оси пары Е; w5 - по оси пары D.

Направление угловой скорости сателлита 3 определяется соотношением величин угловых скоростей w2 и w32.

Рассмотрим три режима движения автомобиля:

• прямолинейное движение w4 = w5 (векторная диаграмма на рис.15.8a). В этом режиме движения корпус дифференциала 2 и полуоси 4 и 5 вращаются с одинаковыми угловыми скоростями w4 = w5 = w2, а относительная угловая скорость сателлита w32=0.
• поворот автомобиля направо w4 < w5 (векторная диаграмма на рис.15.8б). При повороте направо угловые скорости полуосей не равны и связаны неравенством w4 < w5, поэтому сателлит будет вращаться с такой угловой скоростью w32, которая обеспечивает постоянство угловой скорости корпуса дифференциала w2.
• буксование левого колеса w4 = 0 (векторная диаграмма на рис.15.8в). При буксовании левого колеса, правое колесо останавливается w4 = 0, а левое будет вращаться с угловой скоростью w5 = 2∙w2.

Для того, чтобы в условиях низкого сцепления колес с грунтом, уменьшить опасность их пробуксовывания в дифференциалы автомобилей высокой проходимости включают элементы трения или блокировки.

Дата добавления: 2013-12-13