Двоичная фазовая модуляция (ВРSK)

Модуляторы систем с фазовой модуляцией.

Согласно таблице 2.1при фазовой модуляции (ФМ) мгновенное значение фазы радиосигнала отклоняется от фазы несущего колебания на величину, зависящую от мгновенного значения модулирующего сигнала u(t) (4.1):

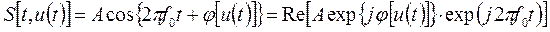(4.4)

Из этого выражения следует, что передаваемая информация b_i сигнала u(t), закодирована в комплексной огибающей

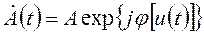(4.5)

передаваемого сигнала S[t,u(t)], которая может быть представлена в полярной (4.5) или квадратурной форме (табл.2.1).

При цифровой модуляции число градаций этого отклонения фазы может быть различным конечным числом. Например, для ФМ-8 возможные значения трех битов слова можно представить группой из восьми разных фазовых углов отклонения фазы.

С учетом общего описания ФМ сигналов (4.4),(4.5) для ФМ-2 на интервале 0 ≤ t ≤ Т_с должны выполнятся соотношения:

для фазы: φ[u(t)] ≡ 0 при u(t) =1, φ[u(t)]≡ π при u(t) ≡ -1, соответственно для комплексной огибающей:

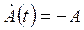при u(t) =1, при u(t) ≡ -1.

Т.о. комплексная огибающая ФМ-2 принимает два значения А и –А на действительной оси комплексной плоскости (сигнального созвездия) и совпадает с b(t).

Для предварительно не фильтрованного НЧ модулирующего сигнала скачки фазы S_m(t) на 180° приводят к расширению полосы и к существенным внеполосным излучениям. На рис.4.2 представлена схема формирования ФМ-2 радиосигнала, где ФНЧ реализуется согласно принципам, изложенным в разд. 4.1.

4 .2.2 Модуляторы систем с квадратурной фазовой манипуляцией (QPSK)

При квадратурной ФМ-4 в модуляторе рис.4.6 каждой паре (из нечетного и четного) входных битов b(t) ставится в соответствие один канальный символ { S_m(t), m=1,2…4 } (радиосигнал) длительностью Т_кс=2Т_с.

S_i(t)=S[t,φ(t)]=A cos[2π f₀t+φ_i(t)]=Re[A exp{j φ_i(t)} exp{j2π f₀t }] (4.6)

Отклонение фазы этого символа от фазы немодулированного несущего колебания φ_i(t)≡π(2i+1)/4 содержит информацию о двух этих входных битах, i =0,1,2,3. При этом комплексная амплитуда (огибающая) этого радиосигнала

(4.7)

на интервале [ 0,2Т_с ] также содержит эту информацию и принимает четыре значения. На рис.4.5а представлен квадратурный принцип

образования этой комплексной амплитуды из последовательности

входных прямоугольных модулирующих электрических импульсов длительностью 2Т_с со значениями +1 или -1.

	b(t)
		Бит

Т_с

Рис.4.5.а. Формирование квадратур модулированной огибающей QPSK и O- QPSK.

Действительная I(t) (нечетные биты) и мнимая Q(t) (четные биты) части этих импульсов образованы расширением до 2Т_с из нечетных и четных номеров последовательности входных битов.

Эти действительная и мнимая части используются для модуляции квадратур несущего колебания

exp{j2π f₀t }=сos (2π f₀t)+jsin (2π f₀t).

Покажем, что таким образом можно получить ФМ-4 модулированный сигнал как в квадратурной форме (2.49), так и в полярной.

При модуляции первой квадратуры можно записать:

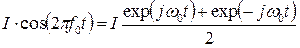
аналогично, для второй:

Тогда модулированный сигнал можно записать в виде (умножая и деля на j вторую квадратуру):

S[(t),φ(t)] = Icos (ω₀t)+ jQsin (ω₀t)=1/2[(I+jQ)· exp (jω₀t)+(I-jQ)· exp (- jω₀t)]

Если ввести обозначения:

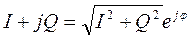
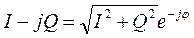
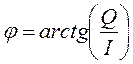, то получим полярную форму

S[(t),φ(t)] =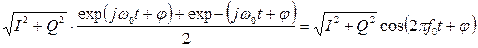(4.8)

Отметим, что меняя значения I и Q, можно получить амплитудную и фазовую модуляцию (при АМ I и Q изменяются пропорционально).

Если I и Q принимают значения +1 или -1, то амплитуда такого сигнала(4.8) –постоянна и равна √2, а фаза φ принимает значения, показанные на сигнальном созвездии рис.4.5б (в коде Грея).

Рис.4.5. Сигнальное созвездие и фазовые переходы огибающей QPSK и O - QPSK.

(Код Грея - двоичное кодирование упорядоченных символов, при котором

код соседних символов отличается минимальным количеством разрядов, т.е. 1.)

В скобках указаны значения входных битов a(t) пары в коде Грея. Все фазовые углы отстоят друг от друга на 90°.В результате комплексная огибающая ФМ-4 модулированного сигнала (4.7) на интервале 0< t ≤ 2Т_с равна

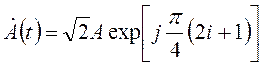, i =0,1,2,3 (4.9)

Структурная схема модулятора ФМ-4 представлена на рис.4.6 (без блока задержки на Т_с в канале Q).

Рис.4.6. Схема модулятора QPSK и O - QPSK.(БЗ на Т_с для O - QPSK.).

Недостатком сигналов QPSK, как и ВPSK, является изменение мгновенной фазы ВЧ модулированного сигнала S_m на 180° и прохождение траектории этого изменения через начало координат. Это приводит при фильтрации ПФ к существенным изменениям амплитуды огибающей сигнала на выходе передатчика (увеличению пик-фактора).

Дата добавления: 2013-12-13