
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
План лекции. 5.1. Понятие определённого интеграла
|
|
|
|
Лекция 5. Определённый интеграл
5.1. Понятие определённого интеграла
5.5. Свойства определённого интеграла
5.5. Оценки определённых интегралов
5.4. Формула Ньютона-Лейбница
5.5. Основные правила интегрирования
5.6. Приближенное вычисление определённых интегралов
5.7. Несобственные интегралы
5.8. Приложения определённого интеграла
5.1. Понятие определённого интеграла
Пусть на интервале ] a, b [ задана непрерывная функция f(x). Разобьем ] a, b [ точками 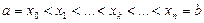 на n элементарных интервалов и составим так называемую интегральную сумму:
на n элементарных интервалов и составим так называемую интегральную сумму:
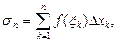 (5.1)
(5.1)
где  - длина k -го элементарного интервала, а
- длина k -го элементарного интервала, а 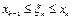 .
.
Обозначим длину наибольшего элементарного интервала через d 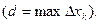
Очевидно из  следует, что
следует, что 
Если существует 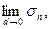 независящий ни от способа разбиения ] a, b [ на элементарные интервалы, ни от выбора точек
независящий ни от способа разбиения ] a, b [ на элементарные интервалы, ни от выбора точек  то он называется определённым интегралом от функции
то он называется определённым интегралом от функции 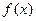 и обозначается
и обозначается 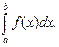 Итак, по определёнию
Итак, по определёнию
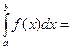
 (5.2)
(5.2)
Геометрический смысл величины sn для функции  показан на рис. 5.1 и представляет площадь ступенчатой фигуры, составленной из прямоугольников с основаниями
показан на рис. 5.1 и представляет площадь ступенчатой фигуры, составленной из прямоугольников с основаниями 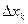 и высотами
и высотами 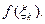
При 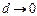 последовательность (sn) площадей этих фигур сходится к площади S криволинейной трапеции a ABb и тем самым
последовательность (sn) площадей этих фигур сходится к площади S криволинейной трапеции a ABb и тем самым
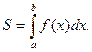 (5.3)
(5.3)
Равенство (5.3) выражает геометрический смысл определённого интеграла. Поскольку  , то в случае
, то в случае 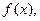 принимающей на ] a, b [ значения с разными знаками, имеем, что
принимающей на ] a, b [ значения с разными знаками, имеем, что
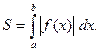 (5.4)
(5.4)
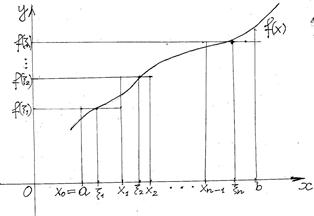
Рис. 5.1
Функция 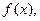 для которой на интервале ] a, b [ существует
для которой на интервале ] a, b [ существует  , называется интегрируемой на ] a, b [.
, называется интегрируемой на ] a, b [.
Непрерывность 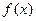 на ] a, b [ достаточна для ее интегрируемости.
на ] a, b [ достаточна для ее интегрируемости.
Функция 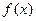 называется кусочно непрерывной на ] a, b [, если она имеет не более конечного числа разрывов первого рода на этом интервале, например, как на рис. 5.5.
называется кусочно непрерывной на ] a, b [, если она имеет не более конечного числа разрывов первого рода на этом интервале, например, как на рис. 5.5.
Рис. 5.2
Кусочно-непрерывные функции также интегрируемы на соответствующих интервалах.
5.5. Свойства определённого интеграла
Из равенства (5.2) вытекают следующие свойства:
1) 

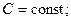
2) 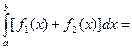
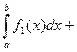

3) 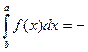
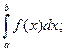
4) 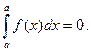
В самом деле, 
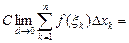

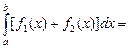
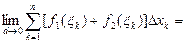
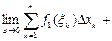
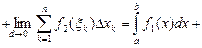
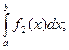
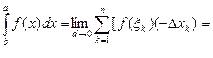
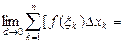

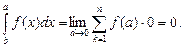
5.5. Оценки определённых интегралов
Покажем справедливость равенства:
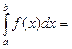

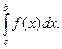 (5.5)
(5.5)
Если 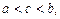 то в качестве одной из точек разбиения ] a, b [ возьмем точку с и получим:
то в качестве одной из точек разбиения ] a, b [ возьмем точку с и получим:
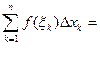
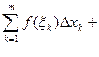
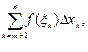 где xm = с. (5.6)
где xm = с. (5.6)
Переходя в (5.6) к пределу при 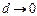 (и
(и  ), имеем соотношение (5.5).
), имеем соотношение (5.5).
Если 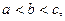 то, полагая xm = b, получим
то, полагая xm = b, получим 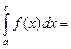

 . Тогда
. Тогда 

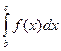 и с учетом свойства 3) приходим к (5.5).
и с учетом свойства 3) приходим к (5.5).
Случай 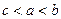 аналогичен.
аналогичен.
Если 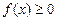 на ] a, b [, то и
на ] a, b [, то и
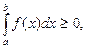 (5.6)
(5.6)
так как 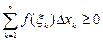 для всех n.
для всех n.
Из  следует, что и
следует, что и
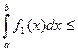
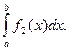 (5.7)
(5.7)
В самом деле, 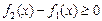 , а тогда
, а тогда 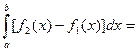
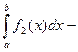
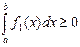 ,
,
что эквивалентно (5.7).
Пусть M и m – наибольшее и наименьшее значения функции f(x) на отрезке [ a, b ]. Поскольку 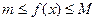 и
и 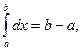 то
то 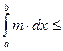

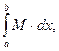
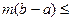
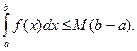 (5.8)
(5.8)
Разделив каждую часть неравенства (5.8) на число (b - a), получим:
 (5.9)
(5.9)
Непрерывная на отрезке функция 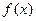 принимает все значения между m и M и, в частности, в некоторой точке
принимает все значения между m и M и, в частности, в некоторой точке  свое значение
свое значение 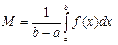 , то есть
, то есть 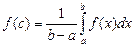 . В силу этого
. В силу этого
 (5.10)
(5.10)
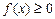 заключается в том, что прямоугольник а CDb с основанием (b - a) и высотой
заключается в том, что прямоугольник а CDb с основанием (b - a) и высотой 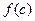 равновелик площади криволинейной трапеции а АВb (рис. 5.3).
равновелик площади криволинейной трапеции а АВb (рис. 5.3).
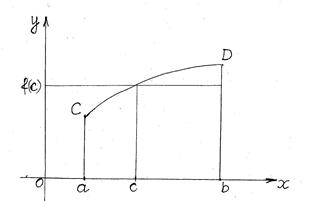
Рис. 5.3
5.4. Формула Ньютона-Лейбница
Функция 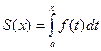 называется интегралом с переменным верхним пределом. Переменная интегрирования обозначена t для избежания путаницы с верхним пределом х.
называется интегралом с переменным верхним пределом. Переменная интегрирования обозначена t для избежания путаницы с верхним пределом х.
Основой для вывода формулы Ньютона-Лейбница является следующее утверждение.
Теорема 5.1. Если функция 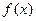 непрерывна на [ a, b ], то одной из ее первообразных является
непрерывна на [ a, b ], то одной из ее первообразных является 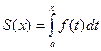 ,
, 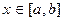 .
.
Доказательство. Задав х приращение 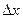 , вычислим приращение
, вычислим приращение 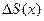 функции
функции 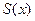 :
: 
Поскольку 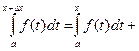
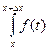 , то
, то 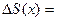
 .
.
По теореме о среднем 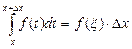 , где
, где 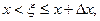 а потому
а потому
 (5.11)
(5.11)
При 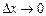 точка
точка  и в силу непрерывности
и в силу непрерывности 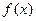 имеем, что
имеем, что 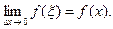 Итак,
Итак, 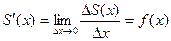 , а это и означает утверждение теоремы 5.1.
, а это и означает утверждение теоремы 5.1.
Если 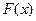 - любая первообразная функция
- любая первообразная функция 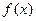 , то
, то
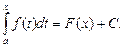 (5.12)
(5.12)
Подставляя  в (5.12), получим:
в (5.12), получим: 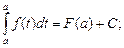
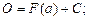
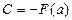 ,
,
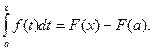
Полагая теперь 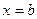 , получим формулу
, получим формулу
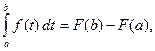 (5.13)
(5.13)
называемую формулой Ньютона-Лейбница.
Эта формула служит мостиком между понятиями неопределённого и определённого интегралов, сводя вычисление последних к нахождению одной из первообразных функции 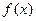 и применению равенства (5.13). Она дает удобный метод вычисления определённых интегралов. По существу только с открытием этой формулы определённый интеграл получил огромное значение в математике и ее приложениях. В силу этого формулу (5.13) называют также основной формулой интегрального исчисления.
и применению равенства (5.13). Она дает удобный метод вычисления определённых интегралов. По существу только с открытием этой формулы определённый интеграл получил огромное значение в математике и ее приложениях. В силу этого формулу (5.13) называют также основной формулой интегрального исчисления.
Рассмотрим примеры.
1. 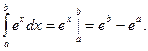
5. 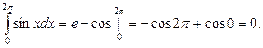
5. 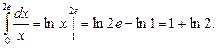
5.5. Основные правила интегрирования
1. Замена переменной в определённом интеграле
Если функция  имеет на интервале
имеет на интервале  непрерывную производную, причем
непрерывную производную, причем 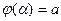 и
и  , то
, то
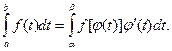 (5.14)
(5.14)
В самом деле, пусть  - первообразная функция
- первообразная функция  , а
, а  - сложная функция. По правилу дифференцирования сложной функции находим
- сложная функция. По правилу дифференцирования сложной функции находим 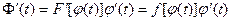 , а потому
, а потому 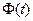 есть первообразная функция
есть первообразная функция 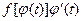 . В силу формулы (5.13) имеем:
. В силу формулы (5.13) имеем:
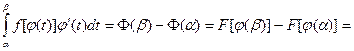
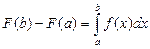 , что и требовалось установить.
, что и требовалось установить.
Заметим, что при замене переменной в определённом интеграле нет необходимости возвращаться к прежней переменной, а лишь следует перейти к новым пределам a и b.
Пример 1. Вычислить  Применим подстановку
Применим подстановку 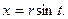 Тогда
Тогда 
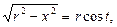
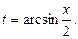 При
При  имеем
имеем 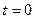 , а при
, а при 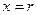 получим
получим 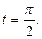 Теперь
Теперь 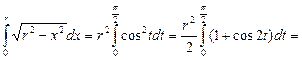
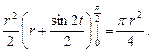
2. Интегрирование по частям определённых интегралов
Если функции  и
и 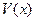 имеют непрерывные производные на интервале ] a, b [, то справедлива формула
имеют непрерывные производные на интервале ] a, b [, то справедлива формула
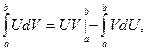 (5.15)
(5.15)
называемая формулой интегрирования по частям в определённом интеграле.
В силу равенства 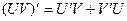 функция
функция 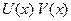 является первообразной функции
является первообразной функции 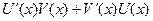 и по формуле Ньютона-Лейбница
и по формуле Ньютона-Лейбница 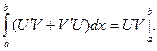 Поскольку
Поскольку  а
а  то
то 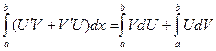 и тем самым
и тем самым 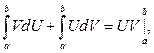 а
а 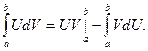
Пример 2. Вычислить 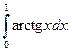
Полагая  имеем
имеем  V = x, а тогда
V = x, а тогда 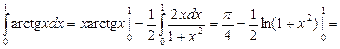

5.6. Приближенное вычисление определённых интегралов
Приближенное вычисление определённых интегралов осуществляется в случаях, когда функция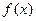 не имеет элементарной первообразной
не имеет элементарной первообразной 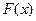 , как, например, такие интегралы:
, как, например, такие интегралы: 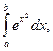
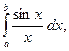

Наиболее употребительны формулы прямоугольников, трапеций и парабол (формула Симпсона). Эти формулы выражают определённый интеграл 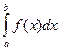 через значения подынтегральной функции
через значения подынтегральной функции 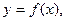 вычисленные для ряда значений аргумента х.
вычисленные для ряда значений аргумента х.
Чаще всего применяется формула Симпсона

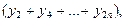 (5.16)
(5.16)
где n – четное число,  Погрешность этой формулы:
Погрешность этой формулы:
 (5.17)
(5.17)
где М – наибольшее значение 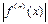 на отрезке [ a, b ].
на отрезке [ a, b ].
Пример 3. Вычислить с точностью до 0,001
При n = 10 имеем h = 0,1. Вычислим значения подынтегральной функции 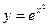 в соответствующих точках деления:
в соответствующих точках деления:
| х 0 = 0 | y 0 = 1,0000 | х 6 = 0,6 | y 6 = 1,4333 |
| х 1 = 0,1 | y 1 = 1,0101 | х 7 = 0,7 | y 7 = 1,6323 |
| х 2 = 0,2 | y 2 = 1,0408 | х 8 = 0,8 | y 8 = 1,8965 |
| х 3 = 0,3 | y 3 = 1,0942 | х 9= 0,9 | y 9 = 2,2479 |
| х 4 = 0,4 | y 4 = 1,1735 | х 10 = 1,0 | y 10 = 2,7183 |
| х 5 = 0,5 | y 5 = 1,2840 |
Подставив найденные значения в формулу (5.16), получим:
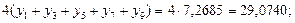
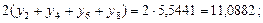
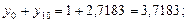
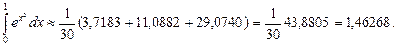
Окончательно получим: 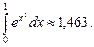
Для функции 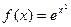 имеем
имеем 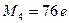 и согласно (5.17)
и согласно (5.17) 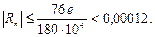
Таким образом, погрешность при n = 10 не превышает 0,00015.
Принцип получения формул приближенного вычисления определённых интегралов основан на их геометрическом смысле и состоит в замене элементарных криволинейных трапеций на более простые плоские фигуры. Замена этих трапеций на прямоугольники порождает формулы
 (5.18)
(5.18)
 (5.19)
(5.19)
Это и есть формулы прямоугольников, смысл которых очевиден из рис. 5.4.
При замене элементарных криволинейных трапеций обычными трапециями приходим к формуле трапеций:
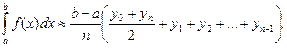 (5.20)
(5.20)
Формула Симпсона получается при замене двух соседних элементарных трапеций на трапецию, ограниченную сверху параболой.
Из рис. 5.4 явствует, что формула трапеций более точна, чем формулы прямоугольников. Заметим, что правая часть в (5.20) есть среднее арифметическое правых частей в (5.18) и (5.19).
В свою очередь формула Симпсона точнее формулы трапеций. При увеличении числа разбиений n отрезка [ a, b ] погрешности каждой из приведенных формул уменьшаются.
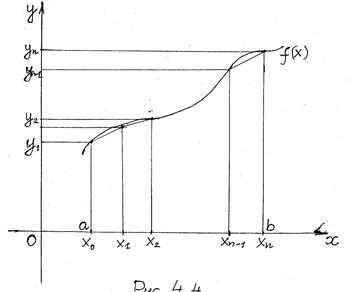
Рис. 5.4
5.7. Несобственные интегралы
Понятие несобственного интеграла связано с обобщением понятия определённого интеграла на случай, когда по крайней мере один из пределов интегрирования бесконечен или подынтегральная функция  терпит бесконечный разрыв в точке
терпит бесконечный разрыв в точке 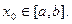
1. Интегралы с бесконечными пределами – это интегралы вида:


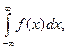 где
где 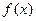 - интегрируемая на любом конечном интервале функция. Полагаем
- интегрируемая на любом конечном интервале функция. Полагаем 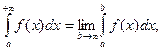
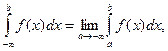
 где С – любое конечное число.
где С – любое конечное число.
2. Интегралы от неограниченных функций.
Если функция 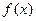 имеет бесконечный разрыв в точке
имеет бесконечный разрыв в точке  , или в точке
, или в точке 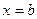 , или в точке
, или в точке  , то по определёнию полагаем:
, то по определёнию полагаем:



Интегралы называются сходящимися, если эти пределы существуют, и расходящимися в противном случае.
Пример 4. Исследовать сходимость интеграла 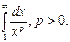
При 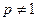 имеем:
имеем: 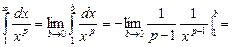
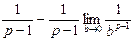 .
.
Если 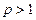 , то
, то 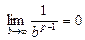 и тогда
и тогда 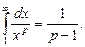 Если
Если 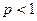 , то
, то 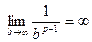 и интеграл расходится. При
и интеграл расходится. При 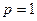
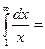
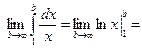

Итак, при 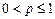 интеграл расходится, а при
интеграл расходится, а при 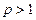 он сходится.
он сходится.
Пример 5. Исследовать сходимость интеграла 
В точке х = 0 функция 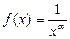 терпит бесконечный разрыв и
терпит бесконечный разрыв и 
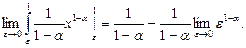 При a < 1
При a < 1 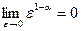 и
и 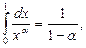 а при a > 1
а при a > 1 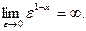
Итак, при a < 1 интеграл  сходится, а если a ³ 1, то интеграл расходится.
сходится, а если a ³ 1, то интеграл расходится.
5.8. Приложения определённого интеграла
1. Вычисление площадей плоских фигур с помощью определённого интеграла непосредственно связано с его геометрическим смыслом, то есть с формулами (5.3) и (5.4).
Пример 6. Вычислить площадь плоской фигуры, ограниченной линиями  и
и 
Решая систему уравнений  вычислим абсциссы точек пересечения кривых.
вычислим абсциссы точек пересечения кривых.
Имеем 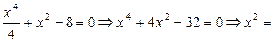
 , то есть
, то есть 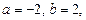 а потому
а потому 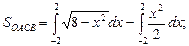

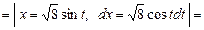
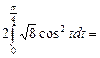
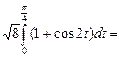

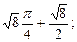
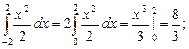

Пример 7. Найти площадь плоской фигуры, ограниченной одной аркой циклоиды 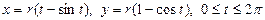 и осью Ох.
и осью Ох.
Поскольку 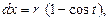 то
то 
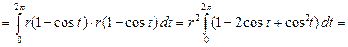

Вычисление площадей многих плоских фигур удобно проводить в полярных координатах 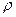 и
и 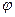 .
.
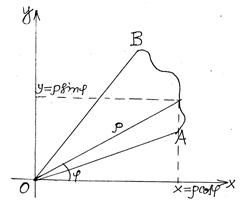
Рис. 5.5
Из рис. 5.5 очевидно, что 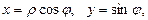 а
а 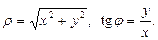
Фигура, изображенная на рис. 5.5, называется криволинейным сектором.
Разбив сектор ОАВ на элементарные криволинейные секторы и заменив их круговыми секторами, получим интегральную сумму 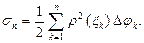
Переходя в ней к пределу при 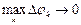 , получим, что площадь сектора ОАВ выражается определённым интегралом
, получим, что площадь сектора ОАВ выражается определённым интегралом
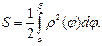 (5.21)
(5.21)
Пример 8. Вычислить площадь фигуры, ограниченной первым витком спирали Архимеда 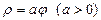 и полярной осью.
и полярной осью.
В этом случае 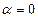 , а
, а 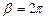 и по формуле (5.21) имеем, что
и по формуле (5.21) имеем, что
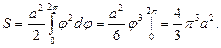
2. Рассмотрим приложения определённого интеграла к некоторым экономическим задачам.
Пример 9. Производство продукции характеризуется темпом роста ее выпуска: 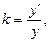
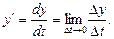
Здесь 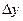 - прирост продукции за время
- прирост продукции за время  , а
, а 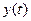 - уровень ее производства за некоторый промежуток времени (например, за год).
- уровень ее производства за некоторый промежуток времени (например, за год).
Найти количество выпущенной за 10 лет продукции при 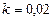 (2% ежегодного темпа роста) и известном в начальный момент времени t = 0 уровне
(2% ежегодного темпа роста) и известном в начальный момент времени t = 0 уровне 
Поскольку 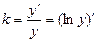 , то, интегрируя это равенство от 0 до t, имеем
, то, интегрируя это равенство от 0 до t, имеем 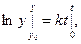
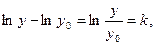
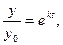
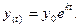 Тогда количество продукции, выпущенной за время t, выражается определённым интегралом:
Тогда количество продукции, выпущенной за время t, выражается определённым интегралом:
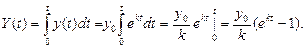
При k = 0,02 и t = 10 лет получим: 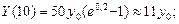

то есть уровень производства увеличится более чем на 22%.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 463; Нарушение авторских прав?; Мы поможем в написании вашей работы!