Бесконечно малые последовательности

Надчисловыми последовательностями можно производить арифметичесие действия.

Определение 2 Пусть и - числовые последовательности. Тогда числовая последовательность 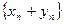называется их суммой +, 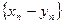- их разностью -, - их произведением , а если для всех номеров n выполняется неравенство , то последовательность 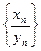называется частным 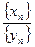данных последовательностей.

Произведение числовой последовательности на некоторое действительное число 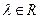можно рассматривать как произведение числовой последовательности на стационарную последовательность :

.

Определение 3 Числовая последовательность, предел которой равен нулю, называется бесконечно малой.

1с. Любая конечная линейная комбинация бесконечномалых является бесконечно малой.

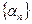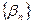Д-во. Пусть числовые последовательности и - бесконечно малые, т.е. , а λ и μ – какие-либодействительные числа. Покажем, что последовательность 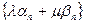- также бесконечно малая. Зададим произвольно и выберем число с так, что . Тогда, согласно определению предела, существует такой номер n₀, что для всех номеров n>n₀ выполняются неравенства 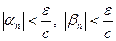и,следовательно, неравенство .

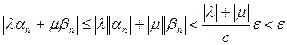Это значит, что 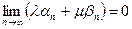. Соответствующее утверждение для любойконечной линейной комбинации бесконечно малых следует из доказанного методом математической индукции.■

2с. Произведение бесконечно малой последовательности на ограниченную последовательность является бесконечно малой.

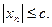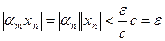Д-во Пусть и { x_n } – ограниченная последовательность, т.е. существует такое с>0, что для всех номеров n выполняется неравенство Зафиксируем произвольное , тогда, согласно определению предела, из условия о бесконечной малости последовательности следует, что существует такой номер n₀, что для всех номеров n>n₀ имеет место неравенство Следовательно, . Это и означает, что , т.е., что последовательность { a_nx_n } – бесконечно малая.■

Следствие. Произведение конечного числа бесконечно малыхпоследовательностей является бесконечно малой.

Д-во. Если , то последовательность 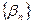, имея конечный предел, является ограниченной последовательнотью. Поэтому произведение 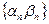бесконечно малых последовательносте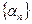й и 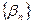можно рассматривать как произведение бесконечно малой последовательности на ограниченную, и следовательно, их произведение по свойству 2 является бесконечно малой. Соответствующее утверждение для любого конечного числа бесконечно малых следует из доказанного методом математической индукции.■

Дата добавления: 2013-12-13