Случайное событие и вероятность его появления

Лекция 52. Основные понятия теории вероятности. Непосредственное вычисление вероятностей случайных событий. Основные правила и формулы комбинаторика.

В окружающей нас жизни есть много чего такого, что невозможно предсказать заранее. Например, невозможно точно предсказать:

· погоду в предстоящий день;

· исход футбольного матча;

· сторону, которой выпадет подброшенная монета;

· оценку на предстоящем экзамене;

· Процент выполнения производственного задания, ход его выполнения, качество выполнения, и так далее.

Такого рода события, величины, процессы называются случайными. Их случайность связана с тем, что многие факторы, их определяющие, нам не известны. Или этих факторов слишком много, что не позволяет все их учесть. Случайные события, величины, процессы изучает специальная наука - теория вероятностей.

Отметим сразу, что теория вероятностей не ставит задачу предсказать, произойдет или не произойдет интересующее нас случайное событие (скажем, выигрыш в лотерею), или какой будет случайная величина (сумма выигрыша), или как пойдет интересующий нас процесс (производственный, политический, и т. д.), да и не может эту задачу решить. Но при большом числе опытов (испытаний) по наблюдению за случайными явлениями в результатах испытаний обнаруживаются определенные закономерности. Изучением этих закономерностей и занимается теория вероятностей.

Исторически теория вероятностей зарождалась как теория азартных игр. В частности, как теория игры в кости (Гюйгенс, Паскаль, Ферма, 17 век).

Следующий этап развития теории вероятностей связан с именем швейцарского математика Якова Бернулли (вторая половина 17-го века), который доказал основную теорему вероятности - «закон больших чисел». После открытия этого закона теория вероятностей становится уже наукой.

Крупнейшими представителями этой науки в 18 веке и первой половине 19-го века были французские математики Лаплас и Пуассон и немецкий математик Гаусс.

Особенно быстро тория вероятностей развивалась во второй половине 19-го и 20-м веке в связи с возникновением и развитием другой вероятностной науки – математической статистики, основы которой мы тоже рассмотрим (во второй части этого курса).

В развитие теории вероятностей и математической статистики крупный вклад внесли и наши отечественные ученые. В первую очередь это члены знаменитой Петербургской математической школы П.Л.Чебышев, А.М.Ляпунов, А.А.Марков (конец 19-го - начало 20-го века). А также работавшие уже в советское время академики А.Н.Колмогоров, С.Н.Бернштейн, А.Н. Хинчин, Н.В. Смирнов и др. Из западных ученых развитие теории вероятностей и математической статистики в наибольшей степени связано с именами английских и американских ученых Стьюдента, Фишера, Пирсона и некоторых других.

В настоящее время теория вероятностей и математическая статистика принадлежат к числу важнейших разделов математики и широко применяются в самых различных отраслях науки и техники. Например, в биологии (исследование процессов гибели и размножения живых организмов); в теоретической физике (физика микромира, статистическая физика); в военном деле (теория стрельб); в машиностроении (теория надежности механизмов и машин); в экономике (организация и планирование производства), и т.д. В связи с такой широтой области применения теории вероятностей и математической статистики и в связи с их все возрастающим значением эти науки входят в настоящее время в учебные программы практически всех инженерно-технических, технологических, экономических, сельскохозяйственных и многих других вузов. И если не каждому специалисту в своей практической деятельности приходится применять вероятностные методы, то уж знакомство с основными понятиями и идеями вероятностных методов необходимо каждому – хотя бы для того, чтобы понимать выводы и рекомендации, вытекающие из использования этих методов.

Определение . СобытиеАназывается случайным, если заранее, до производства испытания (эксперимента, наблюдения) неизвестно, произойдет оно или нет.

Примеры:

1) Испытание - покупка лотерейного билета; случайное событие А – выигрыш по этому билету.

2) Испытание - выстрел стрелка по мишени; случайное событие А – попадание стрелка в мишень.

3) Испытание - подбрасывание монеты; случайное событие А - выпадение орла.

4) Испытание - приход студента на экзамен; случайное событие А – сдача им экзамена.

5) Испытание- посадка в землю семени; случайное событие А – прорастание семени.

Интересующее нас случайное событие А может иметь как большую возможность (много шансов) для своего появления, так и не очень. Если известно, что в повторяемых испытаниях событие А наступает часто – у него, естественно, будет большая возможность появления в каждом отдельном испытании. А если редко - то небольшая.

Возникает естественная задача численной оценки (оценки числом) степени возможности появления в отдельном испытании любого интересующего нас случайного события А. Для решения этой задачи в теории вероятностей разработано понятие вероятности появления случайного события А в единичном испытании. Связывается это понятие со средней долей появления события А в сериях повторных испытаний.

Пусть n – число повторных испытаний (число купленных лотерейных билетов, число выстрелов по мишени, и т.д.), а 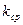– среднее число появлений события А в этих n повторных испытаниях (среднее число выигрышных билетов из n купленных билетов, среднее число попаданий в мишень при n выстрелах по мишени, и.т.д.). Тогда, по определению, в качестве вероятности p(А)появления события А в одном испытании принимается величина

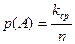(1)

То есть – это средняя доля появлений события А в повторных испытаниях.

Кстати, если известен средний процент появления события А в повторных испытаниях, то среднюю долю появления события А, а следовательно, и его вероятность появления в каждом отдельном испытании можно получить и по такой, вытекающей из (1), формуле:

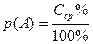(2)

Пусть, например, случайное событие А - это попадание стрелка в мишень. И пусть из опытов известно, что из каждых 10 выстрелов (испытаний) стрелок попадает в цель в среднем 7 раз. Тогда средняя доля попадания стрелка в мишень при повторении выстрелов равна 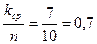. Это и есть, согласно (1), вероятность попадания стрелка в мишень с одного выстрела: = 0,7.

Можно рассудить и по-другому: если стрелок попадает в мишень в среднем 7 раз из 10, то это значит, что он в среднем попадает 70 раз из 100, то есть в среднем в 70% выстрелов. А значит, 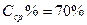, откуда по формуле (2) получаем: = 0,7. То есть получаем тот же самый результат.

Обратно, зная, что вероятность попадания стрелка в мишень с одного выстрела (в одном испытании) равна 0,7, на основании формул (1) и (2) делаем вывод, что средняя доля попаданий такого стрелка в мишень при повторных выстрелах равна 0,7. А это значит, что этот стрелок попадает в мишень в среднем 7 раз из 10, или 70 раз из 100, или 700 раз из 1000, то есть в среднем в 70 % выстрелов.

На практике, то есть с помощью реально проводимых испытаний, среднюю долю появления события А, а следовательно, и вероятность появлений события А в одном испытании можно, очевидно, найти лишь приближенно, ибо реальная доля появлений события А в сериях повторных испытаний от серии к серии меняется. Для достаточно надежного определения этой доли должно быть произведено много повторных испытаний (чем больше, тем лучше). Но в некоторых случаях указанную долю, а значит, и вероятность появления события А в одном испытании можно найти чисто умозрительно, без производства повторных испытаний. Причем найти не приближенно, а точно.

Пусть, например, нам известны все возможные исходы одного испытания, а, следовательно, мы знаем и их общее число n (полагаем, что n - число конечное). И пусть все эти исходы заведомо равновозможны. Равновозможность исходов означает отсутствие каких-либо преимуществ по появлению у каждого исхода испытания по сравнению с любым другим возможным исходом. Равновозможные исходы испытания при повторении испытаний появляются в среднем одинаково часто.

Далее, пусть известно число m тех исходов, которые благоприятствуют появлению интересующего нас события А (это значит, что известно общее число m тех исходов испытания, при осуществлении которых автоматически появляется событие А). При повторении испытаний равновозможные исходы испытания будут наступать в среднем одинаково часто. А значит, если испытаний будет n, то каждый из возможных исходов испытания появится в среднем один раз. Тогда событие A в любых n испытаниях будет появляться в среднем m раз. То есть 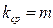. А тогда из формулы (1) получаем:

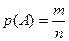(3)

Формула (3) называется классической формулой. Напомним, что в ней n – число всех возможных исходов испытания, а m – число благоприятствующих событию A исходов. Ее можно применять лишь в том случае, когда все n возможных исходов испытания равновозможны. Классическая формула (3) позволяет находить вероятности случайных событий без производства испытаний, чисто умозрительно. Причем находить эти вероятности точно.

Пример1. Пусть испытание – это подбрасывание монеты, а событие A - это выпадение орла. В этом испытании два возможных исхода – орел и решка. То есть n = 2. В силу симметрии монеты эти два исхода равновозможны. Из них лишь один исход благоприятствует событию A (m= 1). Тогда по классической формуле (3) получаем:

Полученный результат очевидным образом верен. Действительно, при повторных бросаниях симметричной монеты орел будет выпадать в среднем в 50% бросаний (эта цифра будет другой, если только монета не симметрична, например, погнута). И по формуле (2) получаем то же самое: = 0,5.

Кстати, если подбрасываемую монету нельзя считать симметричной (она как–то деформирована, так что симметрия ее сторон нарушена), то и в этом случае n = 2 – число всех возможных исходов испытания (орел и решка), а m = 1- единственный благоприятствующий событию A исход (орел). Но в данном случае классическую формулу (3) применять нельзя, ибо исходы испытания (орел и решка) не равновозможны. Тогда для определения вероятности выпадения орла при подбрасывании монеты остается один путь: бросать монету много раз (повторять испытания) и искать опытным путем С_ср. % - средний процент выпадения появления события A (выпадения орла). После нахождения этого среднего процента можно будет по формуле (2) нейти искомую вероятность – вероятность выпадения герба при одном бросании данной монеты. Естественно, что таким путем можно найти лишь приближенно (тем точнее, чем больше будет произведено повторных бросаний монеты).

Пример2. Пусть испытание – это подбрасывание игральной кости (кубика с пронумерованными гранями), а событие A – выпадение цифры 5. В указанном испытании 6 возможных исходов, которые все равновозможны (n =6). А m= 1 – один благоприятствующий событию A исход (выпадение пятерки). Тогда по классической формуле (3) получаем: 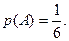Это цифра, в соответствии с формулой (1), означает, что из каждых 6 испытаний (из каждых 6 бросаний кубика) пятерка будет выпадать в среднем один раз. Это совершенно согласуется и со здравым смыслом.

Пример3. Пусть испытание – это вынимание наудачу одной карты из колоды в 36 карт. А событие A – это появление туза (любого). В указанном испытании n= 36 возможных исходов (любая из 36 карт может оказаться вынутой, и вынимание каждой из них – это возможный исход испытания). Все эти исходы, очевидно, равновозможны. А m =4 – число благоприятствующих событию A исходов (в колоде 4 туза). Тогда по классической формуле получаем: 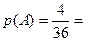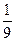. Эта цифра, в соответствии с формулой (1), означает, что из каждых 36 испытаний (опытов по выниманию наудачу одной карты из колоды) событие A (туз) будет появляться в среднем 4 раза. Или, что одно и то же, из 9 испытаний событие A (туз) будет появляться в среднем 1 раз. Это совершенно согласуется и со здравым смыслом.

Примечание. Проведем, для сравнения, и неправильное решение этой же задачи. В указанном испытании всего два возможных исхода (n =2): вынимание туза и вынимание любой другой карты. А m =1 - один благоприятствующий событию А исход. И тогда, по классической формуле, получаем:

Но этот результат неверен, да он и не согласуется со здравым смыслом. Ошибка решения состоит в том, что оба указанные выше возможные исходы испытания не равновозможны, а такие исходы в классической формуле (3) применять нельзя.

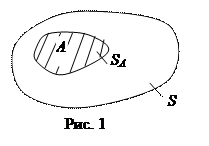
Вероятности появления любого события А можно дать наглядную геометрическую интерпретацию. Для этого условимся представлять себе любое испытание как бросание наудачу точки на некоторую плоскую область площадью S, а событием А будем считать попадание брошенной точки на некоторую часть этой области площадью S_A (рис.1):

При повторных бросаниях средняя доля попаданий брошенной наудачу точки на область А, а значит и вероятность появления события А при каждом отдельном бросании (испытании) будет определяться, очевидно, отношением площадей S_A и S. То есть

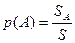(4)

Эту очень полезную в силу ее наглядности геометрическую интерпретацию вероятности появления любого случайного события A мы используем позже, при выводе некоторых важных формул теории вероятностей.

Дата добавления: 2013-12-13