Упражнения. 1. Какой должна быть , чтобы можно было утверждать, что появление события A более вероятно, чем его непоявление?

1. Какой должна быть , чтобы можно было утверждать, что появление события A более вероятно, чем его непоявление?

Ответ: 0,5< 1

2. Доказать свойства (1) – (6) вероятности для тех событий, чьи вероятности можно находить по классической формуле (3).

3. Какова вероятность того, что при двукратном подбрасывании монеты оба раза выпадает орел?

Ответ:

4. Какова вероятность того, что при подбрасывании двух игральных костей сумма выпавших очков будет больше 10?

Ответ: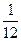

5. Шифр замка автоматической камеры хранения состоит из одной буквы русского алфавита (в нем 33 буквы) и трех цифр (каждая от 0 до 9). Найти вероятность открыть камеру, если набрать шифр наудачу.

Ответ:

6. На круг наудачу брошена точка. Найти вероятность того, что она попадет во вписанный в круг квадрат.

Ответ: 0,64

7. В трапеции с основаниями 6 см и 2 см проведена диагональ, и на трапецию наудачу брошена точка. Каковы вероятности попадания брошенной точки в треугольники, на которые разбилась трапеция?

Ответ: и

8. Каковавероятность того, что первый встречный прохожий родился не весной?

Ответ:

9. Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет имеет окрашенных граней: а) одну; б) две; в) три.

Ответ: а) 0,384; б) 0,096; в) 0,008.

Дата добавления: 2013-12-13