
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Упражнения. Классификация событий. Сумма и произведение событий
|
|
|
|
Классификация событий. Сумма и произведение событий.
Лекция 53-54. Действия с вероятностями случайных событий. Теоремы сложения и умножения вероятностей. Следствия теорем сложения и умножения вероятностей.
Упражнения.
1. В пятом классе изучается 12 предметов. Сколькими способами можно составить расписание занятий на понедельник, если в этот день должно быть 4 урока? Решить задачу в предположении, что:
а) порядок уроков важен;
б) порядок уроков не важен.
Ответ: а) 11880; б) 495.
2. Сколько различных символов можно закодировать с помощью 8-значных двоичных чисел (чисел, содержащих в своей записи лишь нули и единицы общим числом 8)?
Ответ: 256.
3. Пять девушек и пять юношей разыграли 10 мест выделенного им на концерт зрительного ряда (места с 31 по 40). Какова вероятность того, что они будут сидеть строго вперемешку (никакие две девушки и два юноши не будут сидеть рядом)?
Ответ: 1/126.
4. Найти вероятность того, что в лотерее «Спортлото 5 из 36» можно угадать:
а) все 5 номеров; б) 4 номера; в) 3 номера.
Ответ: а) 1/324632; б) 150/324632; в) 4350/324632.
5. Доказать, что вероятность того, что у двенадцати случайно выбранных человек дни рождения приходятся на разные месяцы, меньше 0,0001.
6. Сколькими различными способами можно распределить 6 различных учебников между тремя студентами по два учебника каждому?
Ответ: 90 способами.
7. Набор из 12 пирожных составляется из пирожных 5 видов. Сколькими различными способами можно составить этот набор?
Ответ: 1820 способами.
Определение 1. Два случайных события А и В называются несовместными, если появление одного из них исключает появление другого. В противном случае событие А и В называются совместными.
Пример 1. Попадание А и непопадание В одного и того же стрелка в мишень при одном выстреле – события несовместные.
Пример 2. Попадание А стрелка в мишень в первом выстреле и промах В во втором – события совместные.
Определение 2. Два случайных события А и В называются независимыми, если вероятность появления каждого из них не зависит от того, появится или не появится другое событие. В противном случае события А и В называются зависимыми.
Отметим сразу, что несовместные события всегда зависимы. Действительно, пусть А и В – несовместные события. Тогда при появлении события А появление события В невозможно, а значит 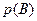 = 0. А при непоявлении события А появление события В возможно, и тогда
= 0. А при непоявлении события А появление события В возможно, и тогда 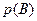 ≠ 0. Таким образом, вероятность появления события В зависит от того, появится или не появится событие А. Следовательно, несовместные события А и В действительно являются зависимыми.
≠ 0. Таким образом, вероятность появления события В зависит от того, появится или не появится событие А. Следовательно, несовместные события А и В действительно являются зависимыми.
А вот если события А и В совместные, то они могут быть как зависимыми, так и независимыми. Подтвердим это на примере.
Пример 3. Пусть из колоды игральных карт (36 карт) вынимают наудачу одну за одной две карты. И пусть событие А состоит в том, что первая вынутая карта окажется тузом, а событие В – что и вторая карта окажется тузом. Рассмотрим два варианта испытания:
а) первая вынутая карта возвращается в колоду;
б) первая вынутая карта не возвращается в колоду.
Очевидно, что в обоих вариантах события А и В совместны. Исследуем их на зависимость –независимость.
а) В этом варианте вероятность появления события В (вынимания второго туза) не зависит, очевидно, от того, произошло или не произошло перед этим событие А (вынимание первого туза) и равна 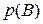 = 4/36=1/9. Следовательно, в варианте а) имеем совместные и независимые события А и В.
= 4/36=1/9. Следовательно, в варианте а) имеем совместные и независимые события А и В.
б) В этом варианте, если событие А произошло, то 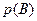 = 3/35 (останется 35 карт, и из них три туза). А если событие А не произошло (первая вынутая карта тузом не оказалась), то
= 3/35 (останется 35 карт, и из них три туза). А если событие А не произошло (первая вынутая карта тузом не оказалась), то 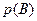 = 4/35 (останется 35 карт, и из них четыре туза) Следовательно, в варианте б) имеем совместные и зависимые события А и В.
= 4/35 (останется 35 карт, и из них четыре туза) Следовательно, в варианте б) имеем совместные и зависимые события А и В.
Связь между совместностью-несовместностью и зависимостью - независимостью двух событий можно изобразить графически в виде схемы (1):
|


|
|
 (1)
(1)
 | ||||||
|
|
Понятия совместности-несовместности и зависимости-независимости обобщаются и на случай группы из нескольких случайных событий (А1; А2; …Аn)
Определение 3. События (А1; А2; …Аn) называются попарно несовместными, если появление каждого из них исключает появление любого другого (то есть если любая пара из группы событий (А1; А2; …Аn) несовместна). В противном случае события (А1; А2; …Аn) называются совместными.
Определение 4. События (А1; А2; …Аn) называются независимыми в совокупности, если каждое из этих событий и любое другое событие, состоящее в появлении и непоявлении остальных событий, являются событиями независимыми. В противном случае события (А1; А2; …Аn) называются зависимыми.
Пример 4. Пусть из коробки, содержащей три шара (синий, красный, зелёный) наудачу по одному вынимают три шара, каждый раз опуская вынутый шар в коробку. И пусть (А; В; С) – события, состоящие в вынимании последовательно синего, красного и зелёного шара. Очевидно, что эти три события – совместные и независимые в совокупности.
Если же вынутые шары в коробку не возвращать, то события (А; В; С) – совместные и зависимые.
Сумма и произведение событий
Определение 5. Суммой случайных событий (А1; А2; …Аn) называется событие В
А1 + А2 +…. Аn = В, (2)
состоящее в появлении хотя бы одного из складываемых событий (или А1, или А2, … или Аn).
Таким образом, в теории вероятности знак сложения (+) означает союз «или».
Определение 6. Произведением случайных событий (А1; А2; …Аn) называется событие С
А1· А2 ···Аn = С, (3)
состоящее в появлении всех перемножаемых событий (и А1, и А2, … и Аn).
Таким образом, в теории вероятности знак умножения (·) означает союз «и».
Пример 5. Пусть (А1; А2; А3) – события, состоящее в попадании в мишень первого, второго и третьего стрелков соответственно. Тогда В = А1 + А2 + А3 – событие, состоящее в попадании в мишень хотя бы одного из стрелков, а С = А1 · А2 ·А3 – событие, состоящее в попадании в мишень всех трёх стрелков.
Суммы и произведения событий обладают следующими очевидными свойствами:
1. А+В=В+А – переместительный закон сложения.
2. (А+В)+С=А+(В+С) – сочетательный закон сложения.
3. А·В=В·А – переместительный закон умножения. (4)
4. (А·В)·С=А·(В·С) – сочетательный закон умножения.
5. (А+В)·С=А·С+В·С – распределительный закон сложения и умножения.
Свойства (4) для случайных событий полностью аналогичны соответствующим свойствам для чисел. Но есть и отличные свойства:
1) А+А=А; 2) А·А=А; 3) (А+В)·А=А; 4) (АВ)·А=АВ. (5)
(продумайте эти свойства самостоятельно).
Определение 7. Символом Ā обозначается событие, противоположное событию А. То есть Ā – это непоявление события А.
Пример 6. Если событие А – попадание стрелка в мишень, то событие Ā – его промах по мишени. Если А – выпадение орла при бросании монеты, то Ā – выпадение решки. Если А – выпадение пятёрки при бросании игральной кости, то Ā – выпадение любой другой цифры. Если событие А – попадание брошенной точки на одноимённую область А (рис.1.1), то событие Ā – непопадание в эту область. И так далее. Очевидно, что
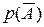 = 1-
= 1- 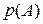 , откуда
, откуда 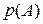 = 1-
= 1- 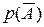 (6)
(6)
Последнее равенство (6) является ещё одной формулой для подсчета вероятностей случайных событий. Ею удобно пользоваться в тех случаях, когда вероятность 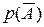 противоположного события Ā найти проще, чем вероятность
противоположного события Ā найти проще, чем вероятность 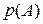 самого события А.
самого события А.
Пример 7. Бросаются две игральные кости. Найти вероятность того, что хотя бы на одной из них не выпадет шестёрка.
Решение. В данной задаче испытание – это бросание двух костей, а событие А – это невыпадение шестёрки хотя бы на одной из них. Событию А благоприятствуют, очевидно, много различных исходов испытания (например, 2-5; 3-6; 6-1, и т.д). И лишь один исход (6-6) благоприятствует событию Ā, противоположному событию А (событие Ā – это выпадение двух шестёрок). Так как всех возможных исходов испытания, очевидно, 36, то по классической формуле
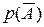 = 1/36.
= 1/36.
Значит, по формуле (6) получаем:
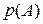 = 1 -
= 1 - 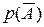 = 1 - 1/36 = 35/36.
= 1 - 1/36 = 35/36.
Событие А (любое) и ему противоположное событие Ā обладают следующими очевидными свойствами:
1) А+Ā – достоверное событие; p(А+Ā) = 1.
2) А·Ā – невозможное событие; p(А·Ā) = 0. (7)
1. Бросаются две игральные кости. Какова вероятность того, что:
а) Сумма выпавших очков будет больше 10?
б) Сумма выпавших очков будет не больше 10?
Ответ: а) 1/12; б) 11/12.
2. Бросаются две игральные кости. Какова вероятность того, что
а) Произведение выпавших очков будет чётным?
б) Произведение выпавших очков будет нечётным?
Ответ: а) 3/4; б) 1/4.
3. Какова вероятность того, что первые три встречные прохожие:
а) Родились в один день?
б) Родились в разные месяцы?
в) Родились летом?
г) Хотя бы один из них родился летом?
д) Никто из них летом не родился?
Ответ: а) 1/144; б) 55/72; в) 1/64; г) 37/64; д) 27/64.
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 739; Нарушение авторских прав?; Мы поможем в написании вашей работы!