Упражнения. Формулы сложения и умножения вероятностей

Но

Но

Формулы сложения и умножения вероятностей.

Формулы сложения и умножения вероятностей – это формулы для нахождения вероятностей сумм и произведений событий. Наиболее просто и наглядно устанавливаются эти формулы с помощью геометрической интерпретации вероятности случайного события, выраженной формулой и рисунком

1. Формула сложения вероятностей двух несовместных событий.

Пусть А и В – любые несовместные события. Геометрически их можно интерпретировать (изобразить) как попадание брошенной наудачу точки на непересекающиеся одноимённые области А и В соответственно (рис. 2):

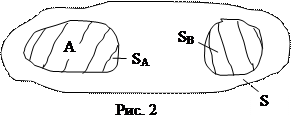Пусть S – площадь всей пластинки, на которую наудачу бросается точка, а S_А и S_B – площади областей А и В соответственно. Рассмотрим сумму С = А+В событий А и В. По определению суммы событий, событие С состоится в появлении хотя бы одного из складываемых событий – или А, или В. То есть событие С = А+В состоит в попадании брошенной точки или в область А, или в область В. Следовательно, в соответствии с формулой получаем:

p(С) = p(А+В) = (S_А+ S_B)/S

(S_А+ S_B)/S = (S_А/S)+(S_B/S) = p(А)+p(В).

Таким образом, если А и В – несовместные события, то

p(А+В) = p(А) + p(В) (8)

2. Формула сложения вероятностей двух совместных событий.

Пусть А и В – любые два совместные события. Геометрически их можно интерпретировать в виде пересекающихся областей А и В соответственно (рис.3). Заметим, что попадание бросаемой точки в общую часть АВ областей А и В означает появление и события А, и события В, то есть представляет собой произведение АВ событий А и В. Именно поэтому общую часть областей А и В мы обозначили символом АВ.

Рассмотрим и здесь сумму С = А+В событий А и В. Согласно рис.3 вероятность появления события С равна отношению суммарной площади, занимаемой областями А и В, к площади S всей пластинки. Но указанная суммарная площадь равна, очевидно, S_А+ S_B – S_АВ (продумайте это!). Поэтому

p(С) = p(А+В) = (S_А+ S_B – S_АВ)/S = S_А/S + S_B /S - S_АВ/S = p(А)+p(В)-p(АВ).

Таким образом, если А и В – совместные события, то

p(А+В) = p(А)+p(В)-p(АВ) (9)

Итак, получаем следующие формулы сложения вероятностей для двух произвольных случайных событий А и В:

p(А+В) = p(А) + p(В) - если А и В несовместны

p(А+В) = p(А)+p(В)-p(АВ) -если А и В совместны (10)

3. Формула умножения вероятностей двух зависимых событий.

Рассмотрим опять рис. 3. События А и В, изображённые на нём – совместные и при этом зависимые. Действительно, совершенно очевидно, что вероятность появления события В зависит от того, произошло или не произошло событие А (попала или не попала брошенная точка в область А).

Подтвердим это. Для этого введём следующие обозначения:

– вероятность появления события В при условии,

что произошло событие А. (11)

– вероятность появления события В при условии,

что не произошло событие А.

Введенные вероятности и называются условными вероятностями события B. Эти вероятности будут одинаковыми, если события A и B независимы (друг от друга), и неодинаковыми, если события A и B друг от другазависимы. Кстати совершенноh аналогично понимаются условные вероятности и события A.

Согласно рис. 3,

; .

Таким образом, . А значит, события A и B зависимые.

А теперь рассмотрим событие D=AB. Согласно рис. 3

.

.

Таким образом, если события A и B зависимые, то

(12)

Кстати, так как 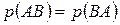, то меняя в равенстве (12) A и B местами, получим еще одну формулу:

(13)

4. Формула умножения вероятностей двух независимых событий.

Если события A и B независимы, то

; .

И тогда на основании и формулы (12), и формулы (4.6) для независимых событий A и B получим:

(14)

Таким образом, получаем следующие формулы умножения вероятностей для произвольных случайных событий A и B:

- если события A и B независимые (15)

- если события A и B зависимые

Формулы (10) и (15) полностью исчерпывают вопрос о формулах сложения и умножения вероятностей для двух случайных событий. Как следует из этих формул, при нахождении вероятности суммы событий важно знать, совместны или несовместны складываемые события A и В. А при нахождении вероятности произведения событий важно знать, зависимы или независимы перемножаемые события А и В.

5. Формулы сложения вероятностей для произвольного числа любых событий.

Полученные выше формулы сложения вероятностей для двух случайных событий можно обобщить и на совокупность из нескольких событий.

Пусть, например, (А; В; С) – любые три попарно несовместные события. Тогда

=

=|учтем, что события А+В и С несовместные|=

==|учтем, что события А и В несовместные|=

=. (16)

И вообще, если имеется n попарно несовместных событий , то

(17)

Если же складываемые события совместны, то подсчет вероятности их суммы сильно усложняется. Например, для трех совместных событий (А; В; С) получаем:

=|учтем, что события А+В и С совместные|= ==

=|учтем, что события АС и ВС совместные|=

==

=|учтем, что |=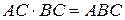

= (18)

Для четырех и более совместных событий вероятность их суммы будет выглядеть еще сложнее. В связи с этим если

- сумма n совместных событий, то вероятность выгоднее искать через вероятность противоположного события по формуле . А так как событие состоит в непоявлении ни одного из событий то 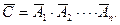И тогда для совместных событий получаем:

(19 )

Таким образом, учитывая (17) и (19), получаем следующие итоговые формулы для вероятности суммы произвольного числа любых случайных событий:

- если события

попарно несовместны (20)

- если события

совместны

6. Формулы умножения вероятностей для произвольного числа любых событий.

Пусть - произвольные случайные события. Если эти события независимы в совокупности, то опираясь на формулу (4.7) для двух событий, получаем:

=

=│учтем, что события и независимы│= (14)

=

Итак, если события независимы в совокупности, то

(15)

Если же эти события зависимы, то опять реализуя схему (14) по последовательному “отщеплению” отдельных событий, но используя уже формулу (4.6), получим:

(16)

Таким образом, учитывая (15) и (16), получаем следующие итоговые формулы для вероятности произведения произвольного числа любых случайных событий:

- если события

независимы в совокупности (17)

- если

события зависимы

А теперь рассмотрим примеры решения задач с применением формул сложения и умножения вероятностей.

Пример 8. Два стрелка по разу стреляют по мишени. Вероятность попадания в мишень для первого стрелка равна 0,7, а для второго 0,8. Найти вероятность того, что

а) в мишень попадут оба; б) оба промахнутся; в) попадет хотя бы один из них; г) попадет только один из них.

Решение. Введем обозначения:

событие А₁ – попадание первого стрелка в мишень;

событие А₂ – попадание второго стрелка в мишень;

событие А – попадание обоих;

событие В – промах обоих;

событие С – попадание хотя бы одного из них;

событие D – попадание только одного из них.

По условию задачи,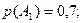

а) Найдем . Очевидно, что Поэтому

│учтем, что события и независимы│=

==0,7·0,8=0,56.

б) Найдем 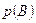. Учтем, что Поэтому

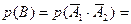|учтем, что события 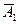и независимы| =

===0,3·0,2=0,06.

в) Найдем . Учтем, что Поэтому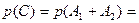

=׀учтем, что события и совместны׀=

=

Заметим, что можно было найти и иначе, если учесть, что =:

г) Найдем . Учтем, что . Поэтому

=׀учтем, что события и несовместны׀ =

==

=│учтем, что множители в обоих произведениях независимы│=

=

Таким образом, из четырех рассмотренных событий (А; В; С; D) наиболее вероятным является событие С – попадание в мишень хотя бы одного из двух стрелков. Его вероятность равна 0,94. Это значит, что в среднем из каждых 100 парных выстрелов будет 94 таких, когда в мишень кто-либо из двух стрелков попадет. А наименее вероятным является событие В – промах обоих. Его вероятность равна 0,06. Это значит, что в среднем из каждых 100 парных выстрелов будет лишь 6 таких, когда оба стрелка промахнутся.

Пример 9. Из колоды в 36 карт наудачу последовательно вынимаются две карты. Какова вероятность того, что они обе окажутся тузами?

Решение. Введем обозначения:

событие А₁ – первая вынутая карта туз;

событие А₂ – вторая вынутая карта туз;

событие А – обе вынутые карты тузы.

Очевидно, что А=А₁·А₂. Поэтому

│учтем, что события и зависимые│=

Примечание. В примере 9, §2 мы рассмотрели эту же задачу, но при условии, что обе карты вынимаются из колоды не по очереди, а сразу (парой). Вероятность того, что они обе окажутся тузами, оказалась той же:. И это совершенно естественно, ибо выбирать какие-то объекты из какой-либо их совокупности по очереди или сразу – это одно и то же и сточки зрения теории вероятностей, и с точки зрения здравого смысла.

Пример 10. На связке 4 ключа. К замку подходит только один ключ. Найти вероятность того, что потребуется не менее трех попыток открыть замок, если опробованный ключ в дальнейших испытаниях не участвует.

Решение. Введем обозначения:

событие А₁ – подойдет первый опробованный ключ;

событие А₂ – подойдет второй ключ;

событие А₃ – подойдет третий ключ;

событие А₄ – подойдет четвертый ключ;

событие А – понадобится не менее трех попыток открыть замок.

Очевидно, что Поэтому

│учтем, что события и несовместны│=

=│учтем, что ; │=

=+ =

=│учтем, что множители – события зависимые│=

==

=.

Впрочем, эту задачу можно было бы решить и гораздо проще. Действительно, ни один из четырех ключей не имеет заведомых преимуществ по сравнению с другими ключами. Поэтому:

.

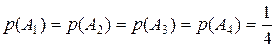А тогда

1. Бросаются три игральные кости. Найти вероятность того, что:

а) На всех трех костях выпадет одинаковое число очков.

б) Произведение выпавших очков будет четным.

в) Сумма выпавших очков будет больше 4.

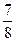Ответ: а); б); в).

2. Отрезок разделен на три равные части. На этот отрезок наудачу брошены три точки. Найти вероятность того, что на каждую часть отрезка попадает по одной точке.

Ответ: .

3. Студент знает 25 из 30 экзаменационных вопросов. Найти вероятность того, что из трех заданных вопросов студент знает: а) не менее двух вопросов; б) все три вопроса.

Ответ: а); б).

4. Четыре человека делают по одной попытке при совершении некоторого действия. Средний процент удачных попыток для них соответственно равен: 30%; 40%; 50%; 60%. Найти вероятность того, что:

а) Все четыре попытки окажутся удачными.

б) Все четыре попытки окажутся неудачными.

в) Хотя бы одна из попыток окажется удачной.

Ответ: а) 0,036; б) 0,084; в) 0,916.

Дата добавления: 2013-12-13