Формула полной вероятности и формула Байеса

Лекция 54. Следствия теорем сложения и умножения вероятностей. Формула полной вероятности и формула Байеса.

Большую часть следствий мы уже рассмотрели в предыдущей главе. Рассмотрим формулу для подсчета вероятности появления хотя бы одного события.

Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий?

Теорема. Вероятность появления хотя бы одного из событий 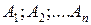, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий :

.

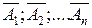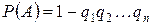Доказательство. Обозначим через А событие, состоящее в появлении хотя бы одного из событий 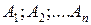. События А и 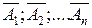(ни одно из событий не наступило) противоположны, следовательно, сумма их вероятностей равна единице: 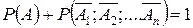. Отсюда, пользуясь формулой умножения, получим 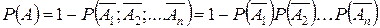, или .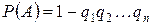

Определение. События 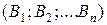образуют полную группу событий, если:

а) они попарно несовместны;

б) одно из них при производстве испытания обязательно произойдет.

Пример 1. События 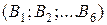, представляющие собой выпадение единицы, двойки,... шестерки при бросании игральной кости, составляют, очевидно, полную группу событий.

Пример 2. Любое случайное событие А и ему противоположное событие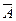составляют очевидно, полную группу событий.

Если события 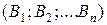составляют полную группу событий, то событие 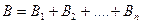, состоящие в появлении хотя бы одного из событий 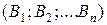, представляет собой достоверное событие. Значит,

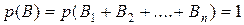(1)

С другой стороны, в силу попарной несовместности событий 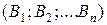по формуле сложения получаем:

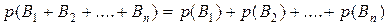(2)

Сравнивая (1) и (2), получаем для полной группы событий :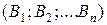

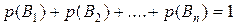(3)

В частности,

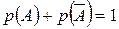, откуда 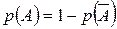( 4)

- формула, приводившаяся ранее.

Если 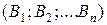- полная группа событий, то любое интересующее нас событие А может произойти лишь совместно с одним из событий этой группы. А значит,

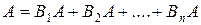(5)

Пусть нам известны вероятности

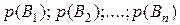(6)

всех событий, составляющих полную группу, а также известны условные вероятности

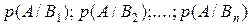(7)

появления события А совместно с каждым из событий этой группы. Тогда из выражения (5) получаем:

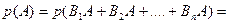
=│учтем, что все слагаемые – это попарно несовместные события│=

=

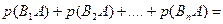
=│учтем, что множители во всех произведениях– зависимые события│=

=

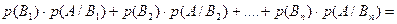
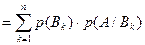(8)

Дата добавления: 2013-12-13