Свойства дисперсии дискретной случайной величины

Для нахождения σ(Х) и V(X)% нужно предварительно найти D(Х) – дисперсию величины Х. При её нахождении полезно знать и использовать свойства дисперсии. Эти свойства таковы:

Свойство 1. Дисперсия постоянной величины равна нулю:

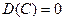(28)

Доказательство. Согласно определения дисперсии (21) и свойства (5) при Х=С получаем:

Свойство (28) имеет очевидный смысл: константа разброса не имеет.

Свойство2. Постоянный множитель выносится из-под знака дисперсии в квадрате:

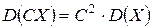(29)

Доказательство. Согласно определения дисперсии (1.21) и свойства (1.6) математического ожидания получаем:

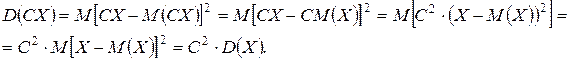
Свойство3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:

(30)

Доказательство. Используя упрощенную формулу (25) для дисперсии и доказанные выше свойства математического ожидания, получим:

Свойство4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

(31)

Доказательство. Оно вытекает из уже доказанных свойств (29) и (30):

Дисперсия случайной величины, как мы знаем, характеризует степень разброса ее возможных значений вокруг ее среднего значения. Свойства 3 и 4, выражаемые равенствами (30) и (31), означают суммирование (увеличение) такого разброса как при сложении двух независимых случайных величин, так и при их вычитании, что вполне естественно.

Следствие 1 свойств 1–4: для любой дискретной случайной величины и для любой константы

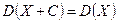(32)

Доказательство. Так как и очевидным образом независимы друг от друга, то

Следствие 2 свойств 1–4: если (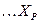) – взаимно независимые случайные величины, то

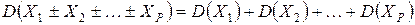(33)

Это следствие докажите самостоятельно (за образец возьмите доказательство аналогичного равенства (13)).

Из наиболее часто используемых числовых характеристик полезно применение моды и медианы случайной величины.

Модой случайной величины называется ее значение, имеющее наибольшую вероятность. В нашем примере = 2.

Медианой случайной величины называется такое ее значение, для которого выполняется следующее условие:

Медиана — такое значение случайной величины, для которого функция распределения равна 0.5.

Упражнения

1. К какому типу случайных величин (дискретным или непрерывным) принадлежат следующие величины:

а) Количество очков, выбиваемых стрелком при стрельбе по мишени в заданной серии выстрелов.

б) Количество студентов студенческой группы, которые сдадут предстоящий экзамен.

в) Процент выполнения предприятием своего производственного задания.

г) Количество осадков, которые выпадут ближайшим летом в данной местности.

Ответ: (а) и (б) – к дискретным, (в) и (г) – к непрерывным.

2. Станок-автомат производит в среднем 10% нестандартных деталей. Наудачу из его продукции отобраны три детали. Написать закон распределения дискретной случайной величины – числа нестандартных деталей среди трех отобранных. Найти , , , .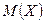

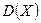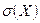Ответ:

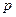
	0,729	0,243	0,027	0,001

; ; ; .

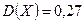3. После ответа студента на вопросы экзаменационного билета экзаменатор задает студенту дополнительные вопросы. Экзаменатор прекращает задавать дополнительные вопросы, как только студент обнаружит незнание заданного вопроса. Вероятность того, что студент ответит на любой заданный дополнительный вопрос, равна 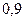. Составить закон распределения дискретной случайной величины – числа дополнительных вопросов, которые задаст экзаменатор студенту. Найти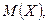

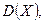
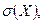
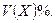
Ответ:

					…		…
					…		…

; ; ; .

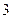
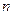
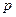
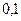
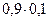
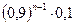
4. Показать, что если – произвольная дискретная случайная величина, а 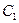и – произвольные константы, то

; ;

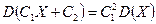5. Брошены две игральные кости. Найти математическое ожидание и дисперсию суммы очков , выпадающих на обеих костях. Причем найти двумя способами:

а) Составив закон распределения суммы очков.

б) Воспользовавшись формулами (8) и (30).

Ответ:

.

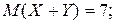
6. Пусть , и 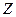– следующие случайные величины: – выручка фирмы (доход от продаж); – ее затраты; – ее прибыль. Найти закон распределения прибыли 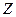, если выручка фирмы и её затраты – независимые случайные величины, заданные законами распределения:

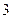
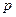
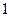
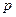
Найти среднее значение прибыли (все суммы – в млн. рублей).

Ответ:

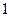
(млн. руб.)

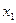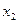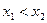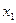7. Дискретная случайная величина имеет только два возможных значения и , причем . Вероятность того, что примет значение , равна . Найти закон распределения величины , если и .

Ответ:

X
p	0,2	0,8

8. Случайные величины X и Y независимы. Найти дисперсию случайной величины Z=2X+3Y, если известно, что D(X)=4, D(Y)=5.

Ответ: D(Z)=61.

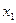9. Дискретная случайная величина Х имеет только три возможных значения: х₁=1, х₂ и х₃, причем . Вероятности того, что Х примет значения и 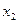соответственно равны 0,3 и 0,2. Найти закон распределения величины Х, зная её математическое ожидание М(Х)=2,2 и дисперсию D(X)=0,76.

Ответ:

X
p	0,3	0,2	0,5

10. Случайная величина задана рядом распределения

X
p	0,14	0,2	0,49	0,17

Найти математическое ожидание М(Х), дисперсию D(X), среднее квадратическое отклонение .

Ответ: М(Х)=6,72, D(Х)=5,682, .

Дата добавления: 2013-12-13