
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Поток событий. Распределение Пуассона
|
|
|
|
Лекция 57. Виды распределений дискретных случайных величин: биномиальное распределение, распределение Пуассона, геометрическое и гипергеометрическое распределения. Простейший поток событий.
Биномиальное распределение.
Пусть  – число появлений некоторого события
– число появлений некоторого события 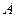 в
в 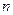 повторных испытаниях, где
повторных испытаниях, где  и
и 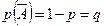 – вероятности появления и непоявления этого события в одном испытании. Очевидно, что
– вероятности появления и непоявления этого события в одном испытании. Очевидно, что  – дискретная случайная величина, у которой (
– дискретная случайная величина, у которой ( ;
; 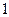 ;
; 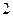 ;
; 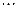
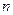 ) – возможные значения, а вероятности (
) – возможные значения, а вероятности ( ;
;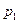 ;
; 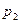 ;
; 
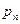 ) этих значений найдутся по формуле Бернулли:
) этих значений найдутся по формуле Бернулли:

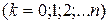 (1)
(1)
Закон распределения

| 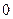
| 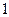
| 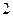
| 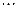
| 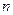
| (2) |
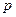
| 
| 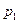
| 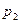
| 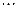
| 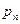
|
такой случайной величины называется биномиальным.
Докажем, что математическое ожидание 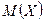 и дисперсия
и дисперсия  случайной величины
случайной величины  , распределенной по биномиальному закону, могут быть найдены по следующим простым формулам:
, распределенной по биномиальному закону, могут быть найдены по следующим простым формулам:
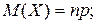
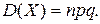 (3)
(3)
Для этого представим величину  в виде суммы
в виде суммы
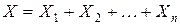 (4)
(4)
Здесь  – это число появлений события
– это число появлений события 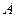 в отдельно взятом
в отдельно взятом 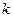 -ом испытании
-ом испытании 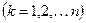 . Закон распределения случайной величины
. Закон распределения случайной величины 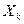 при любом номере
при любом номере 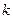 будет, очевидно, иметь вид:
будет, очевидно, иметь вид:
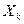
| 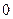
| 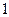
|  (5) (5)
|
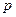
| 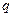
| 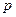
|
Тогда
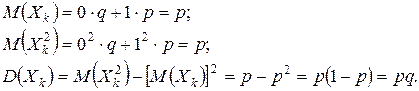 (6)
(6)
Случайные величины (
 ; …
; … ) по смыслу своему независимы друг от друга. Поэтому, опираясь на формулы
) по смыслу своему независимы друг от друга. Поэтому, опираясь на формулы 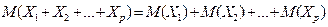 и
и  , получим:
, получим:
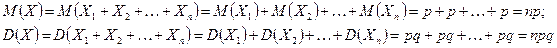 (7)
(7)
Доказательство закончено.
Пример 1. Составить закон распределения случайной величины  – числа выпадений герба при трех бросаниях монеты. Найти
– числа выпадений герба при трех бросаниях монеты. Найти 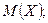
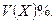
Решение. Так как случайная величина  представляет собой число появлений события
представляет собой число появлений события 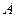 (выпадения герба) при трех повторных испытаниях (при трех бросаниях монеты), то она имеет биномиальный закон распределения:
(выпадения герба) при трех повторных испытаниях (при трех бросаниях монеты), то она имеет биномиальный закон распределения:

| 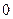
| 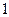
| 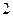
| 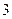
|
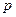
| 
| 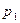
| 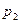
| 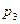
|
Вероятности (


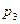 ) найдем по формуле Бернулли при
) найдем по формуле Бернулли при 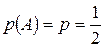 и
и 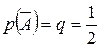 :
:
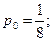
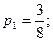

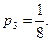
Таким образом, для данной биномиально распределенной случайной величины  получаем следующий закон распределения:
получаем следующий закон распределения:

| 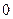
| 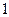
| 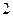
| 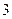
|
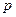
| 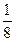
| 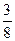
| 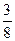
| 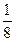
|
Ее числовые характеристики 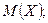
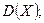
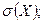
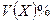 найдем с помощью доказанных выше формул (3):
найдем с помощью доказанных выше формул (3):
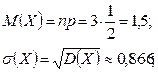
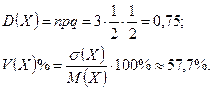
Распределение Пуассона используется в задачах, связанных с потоком событий. Под потоком событий понимают последовательность событий, появляющихся одно за другим в случайные моменты времени. Примерами потоков событий являются: поток звонков на телефонную станцию, в милицию или на станцию скорой помощи; поток заявок в системе массового обслуживания; поток автомобильных аварий на дорогах города и т.д. Поток событий называется простейшим, или пуассоновским, если он характеризуется следующими свойствами:
1) Свойство стационарности. Вероятность появления 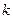 событий потока за промежуток времени длительностью
событий потока за промежуток времени длительностью 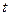 зависит лишь от величины
зависит лишь от величины 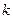 и длительности
и длительности 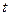 времени, а не от начала отсчета времени.
времени, а не от начала отсчета времени.
2) Свойство ординарности. Вероятность появления двух и более событий за малый промежуток времени пренебрежимо мала по сравнению с вероятностью появления за это время только одного события.
3) Свойство отсутствия последействия. Вероятность появления k событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка.
Можно доказать, что вероятность 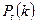 появления
появления 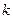 событий простейшего потока за время
событий простейшего потока за время 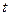 определяется формулой:
определяется формулой:
 (8)
(8)
Здесь 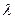 – интенсивность пуассоновского потока, под которой понимается среднее число событий, появляющихся в единицу времени.
– интенсивность пуассоновского потока, под которой понимается среднее число событий, появляющихся в единицу времени.
Пусть  – число событий простейшего потока, происходящих за заданное время
– число событий простейшего потока, происходящих за заданное время 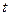 . Очевидно, что
. Очевидно, что  – дискретная случайная величина с возможными значениями (0;1;2;… n,…) и вероятностями (
– дискретная случайная величина с возможными значениями (0;1;2;… n,…) и вероятностями (


 ), находимыми, согласно (8), по формуле:
), находимыми, согласно (8), по формуле:
 где
где 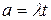
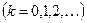 (9)
(9)
Распределение указанной дискретной случайной величины 

| 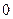
| 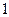
| 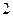
| 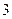
| 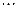
| 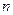
| 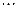
| (10) |
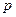
| 
| 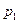
| 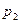
| 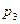
| 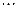
| 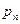
| 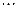
|
называется распределением Пуассона. Его еще называют распределением редких событий. Последнее название связано с тем, что по этой же формуле Пуассона (9), согласно формуле 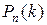
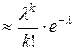 , где
, где 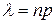 , приближенно находятся вероятности
, приближенно находятся вероятности  появления редкого события k раз в n испытаниях.
появления редкого события k раз в n испытаниях.
Если вычислить числовые характеристики величины  , имеющей распределение Пуассона, то получим (выкладки опускаем):
, имеющей распределение Пуассона, то получим (выкладки опускаем):


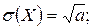
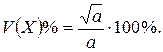 (11)
(11)
Пример 2. Среднее число бракованных деталей, изготавливаемых станком-автоматом в течение одного часа, равно 6. Составить закон распределения дискретной случайной величины  – числа бракованных деталей, которые будут изготовлены станком-автоматом в ближайшие полчаса. Найти числовые характеристики
– числа бракованных деталей, которые будут изготовлены станком-автоматом в ближайшие полчаса. Найти числовые характеристики 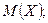
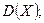
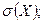
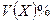 этой случайной величины.
этой случайной величины.
Решение. Будем считать поток бракованных деталей простейшим (пуассоновским). Тогда закон распределения рассматриваемой случайной величины  будет иметь вид (10). При этом вероятности (
будет иметь вид (10). При этом вероятности (

 ) находятся по формуле (9) при
) находятся по формуле (9) при

То есть

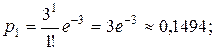
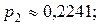

И тогда закон распределения величины  примет вид:
примет вид:

| 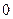
| 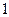
| 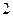
| 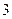
| 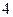
| 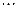
|
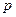
| 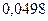
| 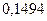
| 
|  
| 
| 
|
А числовые характеристики величины  найдутся по формулам (11):
найдутся по формулам (11):




|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 1749; Нарушение авторских прав?; Мы поможем в написании вашей работы!