Гипергеометрическое распределение

Геометрическое распределение.

Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна p (0<p<1) и, следовательно, вероятность его непоявления q=1-p. Испытания заканчиваются, как только появится событие А. Таким образом, если событие А появилось в k –ом испытании, то в предшествующих k-1 испытаниях оно не появлялось.

Обозначим через Х дискретную случайную величину – число испытаний, которые нужно провести до первого появления события А. Очевидно, возможными значениями Х являются натуральные числа: х₁=1; х₂=2, …

Пусть в первых k-1 испытаниях событие А не наступило, а в k -м испытании появилось. Вероятность этого «сложного события», по теореме умножения вероятностей независимых событий,

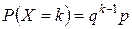. (12)

Полагая k =1,2,…. в формуле (12), получим геометрическую прогрессию с первым членом p и знаменателем q (0<q<1):

p, qp, q²p, …., q^k-1p,…. (13)

По этой причине распределение (13) называют геометрическим. Легко убедиться, что ряд (13) сходится и сумма его равна 1. Действительно, сумма ряда .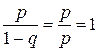

Пример 3. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель p =0,6. Найти вероятность того, что попадание произойдет при третьем выстреле.

Решение. По условию, p =0,6; q =0,4; k =3. Искомая вероятность по формуле (12) .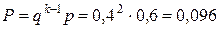

Рассмотрим следующую задачу:

пусть в партии из N деталей имеется М стандартных (М<N). Из партии случайно отбирают n деталей (каждое изделие может быть извлечено с одинаковой вероятностью), причем отобранное изделие перед отбором следующего не возвращается в партию) поэтому формула Бернулли здесь неприменима).

Обозначим через Х случайную величину – число m стандартных изделий среди n отобранных. Очевидно, возможные значения Х таковы: 0,1,2,…, min(M,n). Найдем вероятность того, что Х=m, т.е. что среди n отобранных изделий ровно m стандартных. Используем для этого классическое определение вероятности.

Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь n изделий из N изделий, т.е. числу сочетаний 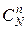. Найдем число исходов, благоприятствующих событию X=m (среди взятых n изделий ровно m стандартных); m стандартных изделий можно извлечь из М стандартных способами; при этом остальные n-m изделий должны быть нестандартными; взять же n-m нестандартных изделий из N-M нестандартных изделий можно способами. Следовательно, число благоприятствующих исходов равно .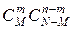

Искомая вероятность равна отношению числа исходов, благоприятствующих событию X=m, к числу всех элементарных исходов

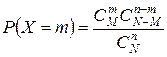. (14)

Эта формула определяет распределение вероятностей, которое называют гипергеометрическим. Как мы видим, оно определяется тремя параметрами: N,M, n. В случае, что если n значительно меньше N (практически если n<0,1N), то гипергеометрическое распределение дает вероятности, близкие к вероятностям, найденным по биномиальному закону.

Пример 4. Среди 50 изделий 20 окрашенных. Найти вероятность того, что среди наудачу извлеченных 5 изделий окажется ровно 3 окрашенных.

Решение. По условию, N=50, M=20, n=5, m=3. Искомая вероятность

.

Дата добавления: 2013-12-13