
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 60. Закон больших чисел. Неравенство Чебышева. Теорема Чебышева
|
|
|
|
Закон больших чисел является центральным законом теории вероятностей в силу того, что он формулирует принципиальную связь между закономерностью и случайностью. А именно, он утверждает, что большое число случайностей ведет к закономерности, что позволяет прогнозировать ход событий. В наиболее общей форме он выражается теоремой Чебышева:
Пусть (Χ1; X2; … Xn; …) независимые случайные величины (их, предполагается, бесконечное число). И пусть их дисперсии равномерно ограничены (то есть дисперсии всех этих случайных величин не превосходят некоторой константы С):
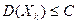
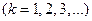 (1)
(1)
Тогда как бы ни было мало положительное число 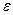 , выполняется предельное вероятностное соотношение:
, выполняется предельное вероятностное соотношение:
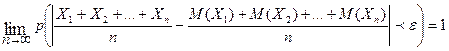 (2)
(2)
если число случайных величин достаточно велико. Или, что одно и то же, вероятность
 (3)
(3)
Таким образом, теорема Чебышева утверждает, что если рассматривать достаточное большое число n независимых случайных величин (Χ1; X2; … Xn),то почти достоверным (с вероятностью, близкой к единице) можно считать событие, состоящее в том, что отклонение среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.
Доказательство. Введем в рассмотрение новую случайную величину 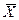 - среднее арифметическое случайных величин (Χ1; X2; … Xn):
- среднее арифметическое случайных величин (Χ1; X2; … Xn):
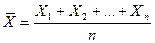 (4)
(4)
Пользуясь свойствами математического ожидания и дисперсии, для 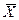 получим:
получим:
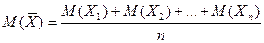 ;
; 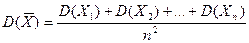 (5)
(5)
Учитывая условия (1), устанавливаем, что
 (6)
(6)
Таким образом, при 
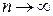 дисперсия
дисперсия 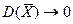 . То есть при
. То есть при 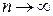 разброс значений случайной величины
разброс значений случайной величины 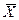 вокруг её математического ожидания
вокруг её математического ожидания 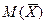 неограниченно уменьшается. А это значит, что при
неограниченно уменьшается. А это значит, что при 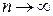 величина
величина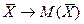 , то есть
, то есть 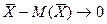 . Или, если сказать точнее, к нулю стремится вероятность того, что случайная величина
. Или, если сказать точнее, к нулю стремится вероятность того, что случайная величина 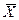 будет хоть как-то отклоняться от своего математического ожидания – константы
будет хоть как-то отклоняться от своего математического ожидания – константы 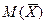 . А именно, при любом сколь угодно малом положительном числе
. А именно, при любом сколь угодно малом положительном числе 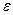
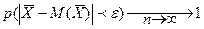 (7)
(7)
Итак, согласно доказанной теореме Чебышева, среднее арифметическое 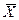 большого числа независимых случайных величин (Χ1; X2; … Xn), являясь случайной величиной, фактически утрачивает характер случайности, становясь, по сути, неизменной константой
большого числа независимых случайных величин (Χ1; X2; … Xn), являясь случайной величиной, фактически утрачивает характер случайности, становясь, по сути, неизменной константой 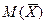 . Эта константа равна среднему арифметическому математических ожиданий величин (Χ1; X2; … Xn). В этом и состоит закон больших чисел.
. Эта константа равна среднему арифметическому математических ожиданий величин (Χ1; X2; … Xn). В этом и состоит закон больших чисел.
Можно привести другое доказательство теоремы Чебышева. Для этого воспользуемся неравенством Чебышева. Оно справедливо и для дискретных и для непрерывных случайных величин и имеет ценность само по себе. Неравенство Чебышева позволяет оценить вероятность того, что отклонение случайной величины от ее математического ожидания не превышает по абсолютной величине положительного числа 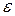 . Приведем доказательство неравенства Чебышева для дискретных случайных величин.
. Приведем доказательство неравенства Чебышева для дискретных случайных величин.
Неравенство Чебышева: Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине меньше положительного числа 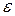 , не меньше, чем
, не меньше, чем 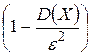 :
:
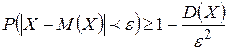 .
.
Доказательство: Так как события, состоящие в осуществлении неравенств 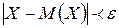 и
и 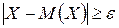 , противоположны, то сумма их вероятностей равна 1, т.е.
, противоположны, то сумма их вероятностей равна 1, т.е. 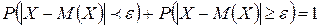 . Отсюда интересующая нас вероятность
. Отсюда интересующая нас вероятность 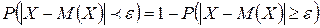 . (*)
. (*)
Найдем 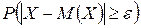 . Для этого найдем дисперсию случайной величины Х.
. Для этого найдем дисперсию случайной величины Х.

Все слагаемые этой суммы неотрицательны. Отбросим те слагаемые, у которых 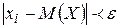 (для оставшихся слагаемых
(для оставшихся слагаемых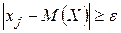 ), вследствие чего сумма может только уменьшится. Условимся считать для определенности, что отброшено k первых слагаемых (будем считать, что в таблице распределения возможные значения занумерованы именно в таком порядке). Таким образом,
), вследствие чего сумма может только уменьшится. Условимся считать для определенности, что отброшено k первых слагаемых (будем считать, что в таблице распределения возможные значения занумерованы именно в таком порядке). Таким образом, 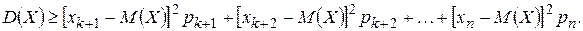
Поскольку обе части неравенства 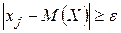 положительны, поэтому, возведя их в квадрат, получим равносильное неравенство
положительны, поэтому, возведя их в квадрат, получим равносильное неравенство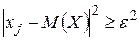 . Воспользуемся этим замечанием, заменяя в оставшейся сумме каждый из множителей
. Воспользуемся этим замечанием, заменяя в оставшейся сумме каждый из множителей 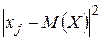 числом
числом 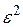 (при этом неравенство может лишь усилиться), получим
(при этом неравенство может лишь усилиться), получим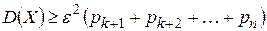 . (**)
. (**)
По теореме сложения, сумма вероятностей 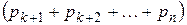 есть вероятность того, что Х примет одно, безразлично какое, из значений
есть вероятность того, что Х примет одно, безразлично какое, из значений 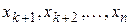 , а при любом из них отклонение удовлетворяет неравенству
, а при любом из них отклонение удовлетворяет неравенству 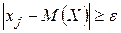 . Отсюда следует, что сумма
. Отсюда следует, что сумма 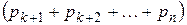 выражает вероятность
выражает вероятность 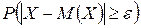 . Это позволяет переписать неравенство (**) так:
. Это позволяет переписать неравенство (**) так: 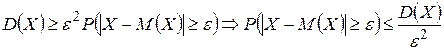 . (***).
. (***).
Подставим (***) в (*) и получим 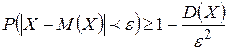 , что и требовалось доказать.
, что и требовалось доказать.
Доказательство теоремы Чебышева 2:
Введем в рассмотрение новую случайную величину 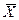 - среднее арифметическое случайных величин (Χ1; X2; … Xn):
- среднее арифметическое случайных величин (Χ1; X2; … Xn):
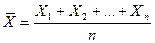
Пользуясь свойствами математического ожидания и дисперсии, для 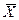 получим:
получим:
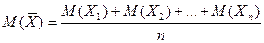 ;
; 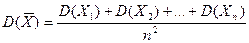 . (*)
. (*)
Применяя к величине 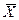 неравенство Чебышева, имеем
неравенство Чебышева, имеем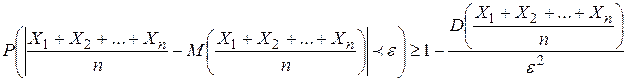 .
.
Учитывая соотношение (*),
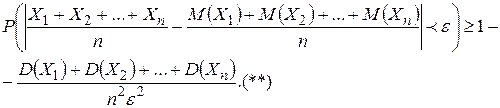
По условию 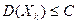
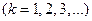 , значит
, значит 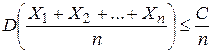 . (***) Подставляя правую часть (***) в неравенство (**) имеем
. (***) Подставляя правую часть (***) в неравенство (**) имеем
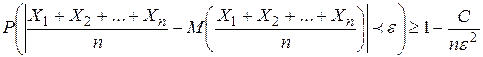 .
.
Отсюда, переходя к пределу при 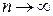 , получим
, получим
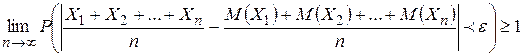 .
.
Поскольку вероятность не может превышать единицу, окончательно мы получаем: 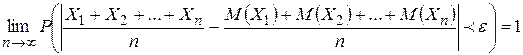
Что нам и требовалось доказать.
Остановимся на одном важном частном случае теоремы Чебышева. А именно, рассмотрим случай, когда независимые случайные величины (Χ1; X2; … Xn) имеют одинаковые законы распределения, а, следовательно, и одинаковые числовые характеристики:
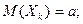
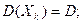
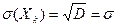
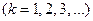 (8)
(8)
Тогда для случайной величины 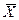 , согласно (5), имеем:
, согласно (5), имеем:
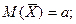
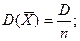
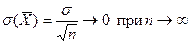 (9)
(9)
Предельное вероятностное соотношение (7) в этом случае примет вид:
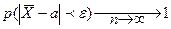 (10)
(10)
Вывод, следующий из (10), имеет большое значение для борьбы со случайными ошибками при производстве различного рода измерений.
Пусть, например, требуется измерить некоторую величину а. Произведем не одно, а несколько (n) независимых повторных измерений значения этой величины. Любым измерениям присуща случайная ошибка, связанная с несовершенством измерительного прибора, всевозможными случайными помехами измерению, и т.д. Поэтому результаты (Χ1; X2; … Xn) отдельных последовательных измерений искомого значения а, вообще говоря, давать не будут - они будут случайными величинами. Причем величинами, имеющими одинаковые распределения, ибо измерения производятся повторно, то есть при неизменных внешних условиях. Тогда для величины 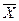 - среднего арифметического из результатов всех n измерений - будет выполняться предельное вероятностное соотношение (10). А значит, это среднее арифметическое
- среднего арифметического из результатов всех n измерений - будет выполняться предельное вероятностное соотношение (10). А значит, это среднее арифметическое 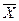 при
при 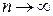 утрачивает характер случайности, превращаясь в а – истинное значение измеряемой величины. Об этом, кстати, свидетельствуют и формулы (9), согласно которым:
утрачивает характер случайности, превращаясь в а – истинное значение измеряемой величины. Об этом, кстати, свидетельствуют и формулы (9), согласно которым:
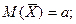
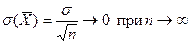 (11)
(11)
То есть проведя достаточно большоечисло повторных измерений искомой величины а, в каждом из которых возможна случайная ошибка измерения, и находя затем среднее арифметическое 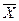 результатов этих измерений, мы по формуле
результатов этих измерений, мы по формуле
а 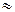
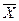 (12)
(12)
можем получить значение а практически без случайной ошибки.
Этот вывод - следствие закона больших чисел. В данном случае этот закон проявляется в том, что при суммировании результатов измерений в (4) случайные ошибки отдельных измерений, встречающиеся в принципе одинаково часто как со знаком плюс, так и со знаком минус, в целом будут взаимно уничтожаться. А оставшаяся ошибка еще разделится на п, то есть еще уменьшится в п раз. Так что при больших значениях n величина 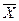 будет практически точно равна измеряемой величине а. Этим выводом, естественно, широко пользуются на практике.
будет практически точно равна измеряемой величине а. Этим выводом, естественно, широко пользуются на практике.
Примечание. В величине 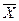 взаимно уничтожаются лишь случайные ошибки измерений, то есть ошибки, связанные с действием случайных факторов (помех). Но систематические (постоянно действующие) ошибки, то есть ошибки, присущие каждому измерению, естественно, остаются и в
взаимно уничтожаются лишь случайные ошибки измерений, то есть ошибки, связанные с действием случайных факторов (помех). Но систематические (постоянно действующие) ошибки, то есть ошибки, присущие каждому измерению, естественно, остаются и в 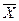 . Например, сбитая (не отрегулированная) в приборе стрелка вызывает постоянную (систематическую) ошибку в каждом измерении, а, значит вызывает её и в средней арифметической
. Например, сбитая (не отрегулированная) в приборе стрелка вызывает постоянную (систематическую) ошибку в каждом измерении, а, значит вызывает её и в средней арифметической 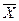 из результатов этих измерений. Систематические ошибки надо исключать еще до производства измерений и не допускать в процессе измерений.
из результатов этих измерений. Систематические ошибки надо исключать еще до производства измерений и не допускать в процессе измерений.
Потом, если α – цена деления измерительного прибора, то все повторные измерения производятся с точностью до α. Но тогда, естественно, и среднее арифметическое 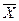 из результатов всех измерений можно указывать лишь тоже с точностью до α, то есть с точностью, определяемой точностью прибора.
из результатов всех измерений можно указывать лишь тоже с точностью до α, то есть с точностью, определяемой точностью прибора.
Поэтому не стоит думать, что, сделав достаточно большое число повторных измерений величины а и найдя затем среднее арифметическое 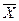 из результатов этих измерений, мы получим точное значение а. Мы его получим лишь в пределах точности измерительного прибора. Да и то, если исключим систематическую ошибку измерения.
из результатов этих измерений, мы получим точное значение а. Мы его получим лишь в пределах точности измерительного прибора. Да и то, если исключим систематическую ошибку измерения.
Приведем еще один важный частный случай закона больших чисел. Пусть Х=k – число появлений некоторого события А в п повторных испытаниях (X – случайная величина). И пусть 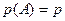 и
и 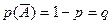 – вероятности появления и непоявления события А в одном испытании. Рассмотрим случайную величину
– вероятности появления и непоявления события А в одном испытании. Рассмотрим случайную величину 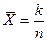 - относительную частоту появления события А в п испытаниях. Введем также n случайных величин (Х1, Х2,…Xn), которые представляют собой число появление события А в первом, втором, … п -ом испытаниях. Тогда k = Х1+Х2+…+Хп, а
- относительную частоту появления события А в п испытаниях. Введем также n случайных величин (Х1, Х2,…Xn), которые представляют собой число появление события А в первом, втором, … п -ом испытаниях. Тогда k = Х1+Х2+…+Хп, а
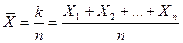
 (13)
(13)
Случайные величины (Х1, Х2,…Xn) имеют одинаковые и простые законы распределения:
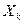
| 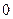
| 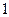
| 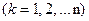 (14) (14)
|
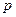
| 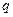
| 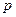
|
Из (14) находим: 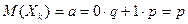 (15)
(15)
Предельное вероятностное соотношение (10) для рассматриваемого случая примет вид:
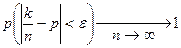 (16)
(16)
То есть при достаточно большом числе п повторных испытаний можно почти наверняка (с вероятностью, близкой к единице) ожидать, что относительная частота 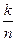 появления события А практически совпадет с вероятностью
появления события А практически совпадет с вероятностью 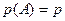 появления события А в одном испытании. На этом выводе основано нахождение вероятностей многих случайных событий, чьи вероятности каким-то другим путем (теоретически) найти не удается.
появления события А в одном испытании. На этом выводе основано нахождение вероятностей многих случайных событий, чьи вероятности каким-то другим путем (теоретически) найти не удается.
Например, пусть испытание – это подбрасывание деформированной (несимметричной) монеты, а событие А для этого испытания – это выпадение герба. Вероятность 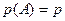 события А по классической формуле
события А по классической формуле 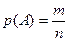 или по какой-то другой теоретической формуле найти затруднительно, ибо в такой формуле должны быть как-то отражены характеристики деформации монеты. Поэтому реальный путь, ведущий к цели, здесь один: повторно бросать монету (чем больше число бросаний n, тем лучше) и определять опытным путем относительную частоту
или по какой-то другой теоретической формуле найти затруднительно, ибо в такой формуле должны быть как-то отражены характеристики деформации монеты. Поэтому реальный путь, ведущий к цели, здесь один: повторно бросать монету (чем больше число бросаний n, тем лучше) и определять опытным путем относительную частоту 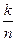 появления герба. Если n велико, то в соответствии с законом больших чисел можно с большой вероятностью утверждать, что
появления герба. Если n велико, то в соответствии с законом больших чисел можно с большой вероятностью утверждать, что 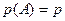
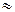
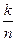 .
.
Закон больших чисел проявляет себя во многих природных и общественных явлениях.
Пример 1. Как известно, газ, помещенный в закрытый сосуд, оказывает давление на стенки сосуда. Согласно законам газового состояния, при неизменной температуре газа это давление постоянно. Давление газа имеет своей причиной хаотические удары отдельных его молекул о стенки сосуда. Скорости и направления движения у всех молекул разные, поэтому разными являются и силы ударов различных молекул о стенки сосуда. Однако давление газа на стенки сосуда определяется не силой ударов отдельных молекул, а их средней силой. Но она, как средняя из огромного числа независимо действующих сил, согласно закону больших чисел, будет сохранять практически неизменное значение. Поэтому практически неизменным оказывается и давление газа на стенки сосуда.
Пример 2. Страховая компания, занимающаяся, например, автострахованием, выплачивает по разным страховым случаям (автомобильным авариям и ДТП) разные страховые суммы. Однако величина среднего значения этой страховой суммы, как среднего значения из многих различных n независимых страховых сумм, согласно закону больших чисел, будет практически неизменной. Ее можно определить, исследовав реальную статистику страховых случаев. Чтобы страховой компании не оказаться в убытке, средний размер страхового взноса, взимаемого с клиентов этой компании, должен быть выше средней страховой суммы, которую выплачивает компания своим клиентам. Но этот взнос не должен быть и слишком высоким, чтобы компания была конкурентноспособна (могла конкурировать по привлекательности с другими страховыми компаниями).
|
|
|
Дата добавления: 2013-12-13; Просмотров: 3724; Нарушение авторских прав?; Мы поможем в написании вашей работы!