
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 61. Функции случайных величин, действия со случайными величинами. Свойства математического ожидания и дисперсии
|
|
|
|
Пусть Y – случайная величина, значение которой полностью определяется значением другой случайной величины X. То есть случайная величина Y является функцией случайной величины X:

 (1)
(1)
Например, если изготавливаются цилиндрические болванки, и X – диаметр болванок (X – случайная величина), то
 (2)
(2)
- площадь поперечного сечения этих болванок, которая тоже является случайной величиной. И эта величина Y – функция величины X. Аналогично доход Y=pX от ежедневных продаж товара – функция от объема X проданного товара, где р – цена единицы товара. И т.д.
Пусть известно распределение случайной величины X (аргумента). Спрашивается, каким будет распределение случайной величины  - функции величины X? Ответ на этот вопрос, очевидно, должен быть отдельным для дискретных и отдельным для непрерывных случайных величин.
- функции величины X? Ответ на этот вопрос, очевидно, должен быть отдельным для дискретных и отдельным для непрерывных случайных величин.
1. Пусть X – дискретная случайная величина, а таблица (3) – закон ее распределения:
| Х | 
| 
| … | 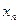
| (3) |
| р | 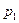
| 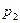
| … | 
|
Тогда  - тоже дискретная случайная величина, а таблица (4) – закон её распределения:
- тоже дискретная случайная величина, а таблица (4) – закон её распределения:

| 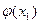
| 
| … | 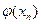
| (4) |
| р | 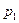
| 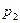
| … | 
|
Действительно, значениями случайной величины  будут значения
будут значения 
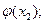 …
…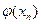 , а вероятности р
, а вероятности р ; р
; р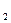 ;...р
;...р у этих значений будут теми же, что и у значений х
у этих значений будут теми же, что и у значений х ; х
; х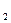 ;...х
;...х . Последние обстоятельство следует из того факта, что события Х=х
. Последние обстоятельство следует из того факта, что события Х=х и
и  ) (i=1,2,…n) наступают или не наступают одновременно. Значит, они имеют одинаковые вероятности.
) (i=1,2,…n) наступают или не наступают одновременно. Значит, они имеют одинаковые вероятности.
Пример 1. Случайная величина Х имеет следующий закон распределения:
| Х | -1 | |||
| р | 0.5 | 0.2 | 0.2 | 0.1 |
Составить закон распределения случайной величины Y=Х .
. 
Решение. Согласно (4) имеем:
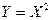
| ||||
| р | 0.5 | 0.2 | 0.2 | 0.1 |
Суммируя вероятности совпадающих значений, получим окончательно:
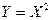
| |||
| р | 0.2 | 0.7 | 0.1 |
После того, как закон распределения функции  составлен, можно, при желании, найти и её числовые характеристики М(Y), D(Y), s(Y), V(Y)
составлен, можно, при желании, найти и её числовые характеристики М(Y), D(Y), s(Y), V(Y) .
.
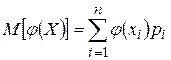 ,
, 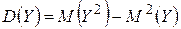 ,
,  ,
,


2. Пусть теперь Х - непрерывная случайная величина, распределение которой задаётся интервалом (a;b) её возможных значений и плотностью вероятности f (х) для х  (a;b). Тогда
(a;b). Тогда  - тоже непрерывная случайная величина. Распределение величины Y будет известно, если мы найдём интервал (с; d) её возможных значений у и плотность вероятности g(у) для у
- тоже непрерывная случайная величина. Распределение величины Y будет известно, если мы найдём интервал (с; d) её возможных значений у и плотность вероятности g(у) для у (с; d).
(с; d). 
Сразу отметим, что интервал (с;d), который содержит все возможные значения у случайной величины  , представляет собой, очевидно, область значений функции у=
, представляет собой, очевидно, область значений функции у= (а<х<b). А плотность вероятности g(у) величины
(а<х<b). А плотность вероятности g(у) величины  будем искать, исходя из следующих соображений.
будем искать, исходя из следующих соображений.
Пусть х - некоторое возможное значение величины Х (а<х<b). Тогда y= (c<y<d) – соответствующее ему значение величины Y. Окружим точку x некоторым бесконечно малым отрезком длиной dx. Тогда этому отрезку, окружающему точку x, будет соответствовать некоторой бесконечно малый отрезок длиной
(c<y<d) – соответствующее ему значение величины Y. Окружим точку x некоторым бесконечно малым отрезком длиной dx. Тогда этому отрезку, окружающему точку x, будет соответствовать некоторой бесконечно малый отрезок длиной  , окружающий точку y (рис. 1)
, окружающий точку y (рис. 1)
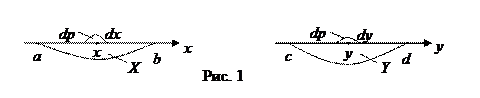
В выражении 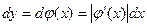 производная
производная 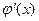 взята по модулю с тем, чтобы выражение для длины dy было верным и для возрастающей функции
взята по модулю с тем, чтобы выражение для длины dy было верным и для возрастающей функции  (когда
(когда  ), и для убывающей (когда
), и для убывающей (когда  ).
).
Попадание значения случайной величины X на отрезок dx будет, очевидно, автоматически означать попадание значения случайной величины Y на отрезок dy. Вероятности dp появления обоих этих событий, таким образом, одинаковы. Следовательно, одновременно имеем:

 (5)
(5)
Сравнивая эти два значения dp, получаем:
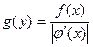 (6)
(6)
Чтобы получить окончательное выражение для g(у), нужно правую часть равенства (6) выразить через у. Для этого из равенства у = , связывающего х и у, нужно х выразить через у. То есть нужно найти функцию х =
, связывающего х и у, нужно х выразить через у. То есть нужно найти функцию х =  , обратную к функции у =
, обратную к функции у =  . Такая обратная функция заведомо существует, если исходная функция у =
. Такая обратная функция заведомо существует, если исходная функция у =  монотонно возрастает или монотонно убывает, что мы и будем предполагать. Найдя функцию x =
монотонно возрастает или монотонно убывает, что мы и будем предполагать. Найдя функцию x =  , можем и производную
, можем и производную 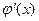 функции у =
функции у = выразить через y:
выразить через y:
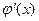 =
=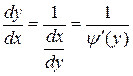 (7)
(7)
С учетом этого функция g(y) причем следующий окончательный вид:
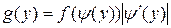 (c<y<d) (8)
(c<y<d) (8)
Это и есть плотность вероятности непрерывной случайной величины Y, являющейся функцией Y = непрерывной случайной величины Х. При этом
непрерывной случайной величины Х. При этом 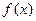 - плотность вероятности величины Х, а x =
- плотность вероятности величины Х, а x = - функция, обратная функции у=
- функция, обратная функции у= 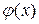 .
.
После того, как найдена плотность вероятности 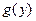 случайной величины
случайной величины  , можно, при желании, найти все числовые характеристики этой величины:
, можно, при желании, найти все числовые характеристики этой величины:
 ;
;  , где
, где  ; (9)
; (9)


Впрочем, для нахождения этих числовых характеристик величины  не обязательно находить функцию g(y). Подставляя в интегралы (9) выражение (8) для g(y) и делая затем подстановку x =
не обязательно находить функцию g(y). Подставляя в интегралы (9) выражение (8) для g(y) и делая затем подстановку x =  , получим (выкладки проделайте самостоятельно):
, получим (выкладки проделайте самостоятельно):
 ;
;
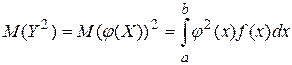 ; (10)
; (10)
 ;
; 

Пример 2. Непрерывная случайная величина Х задана плотностью вероятности 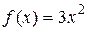 (0
(0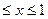 ). Найти плотность вероятности случайной величины Y =
). Найти плотность вероятности случайной величины Y = 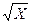 , а также вычислить её основные числовые характеристики.
, а также вычислить её основные числовые характеристики.
Решение. Сначала найдём промежуток  возможных значений у величины Y =
возможных значений у величины Y =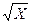 . То есть найдем область значений функции у =
. То есть найдем область значений функции у = (0
(0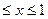 ). Она очевидна: 0
). Она очевидна: 0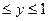 . То есть
. То есть  =
=  .
.
Теперь найдём g(у) (0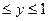 ) – плотность вероятности случайной величины Y. Так как у =
) – плотность вероятности случайной величины Y. Так как у =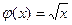 (0
(0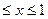 ), то х =
), то х =  (0
(0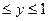 ), а
), а 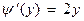 . И тогда, согласно (5.8), получаем:
. И тогда, согласно (5.8), получаем:
 (0
(0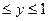 ) (11)
) (11)
А отсюда уже, согласно (9), находим:
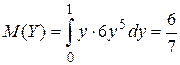 ;
; 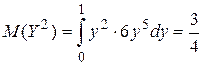 ;
;
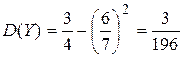 ;
; 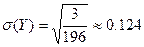 ;
; 
Впрочем, для нахождения числовых характеристик случайной величины Y= 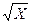 можно было бы применить и формулы (10):
можно было бы применить и формулы (10):
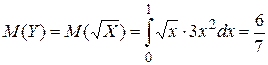 ;
;
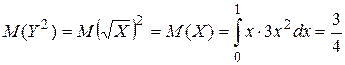 ;
;
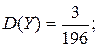
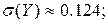

Пример 3. Непрерывная случайная величина X распределена нормально с параметрами (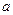 ;
;  ). Доказать, что любая линейная функция Y =
). Доказать, что любая линейная функция Y =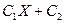 (
(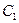
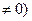 этой величины X тоже распределена нормально с параметрами (
этой величины X тоже распределена нормально с параметрами ( ;
; 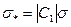 ).
).
Доказательство. Плотность вероятности 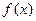 нормально распределенной величины X имеет, как известно, вид:
нормально распределенной величины X имеет, как известно, вид:
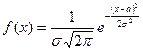 (-
(-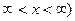
Так как возможные значения x величины X - любые числа от -  до
до  , то и возможные значения у величины Y =
, то и возможные значения у величины Y =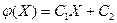 - любые числа. То есть интервал (c; d) возможных значений величины Y – это вся ось oy от -
- любые числа. То есть интервал (c; d) возможных значений величины Y – это вся ось oy от -  до
до  .
.
Теперь найдем g(y) (- <x<
<x< ) - плотность вероятности случайной величины Y. Так как y =
) - плотность вероятности случайной величины Y. Так как y =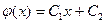 , то x =
, то x = 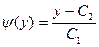 , а
, а  . И тогда, согласно (8), получаем
. И тогда, согласно (8), получаем
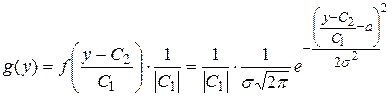 =
=  (-
(-  < y <
< y <  ),
),
где

 .
.
Доказательство закончено.
Для нормально распределенных случайных величин доказан и более общий факт: если (X ; X
; X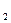 ;…;X
;…;X ) – независимые нормально распределенные случайные величины, то любая их линейная комбинация
) – независимые нормально распределенные случайные величины, то любая их линейная комбинация
Z= 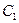 X
X +C
+C …+C
…+C X
X (12)
(12)
тоже является случайной величиной, распределенной нормально. И если ( ) – параметры величин X
) – параметры величин X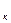 (k = 1, 2,..., p), то параметры (
(k = 1, 2,..., p), то параметры (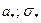 ) величины Z таковы:
) величины Z таковы:

 (13)
(13)
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 432; Нарушение авторских прав?; Мы поможем в написании вашей работы!