Лекция 9. Системы эконометрических уравнений

Литература

1. Буганов В.И. Мир истории: Россия в ХVII столетии. М., 1989.

2. История Отечества: люди, идеи, решения: Очерки ис­тории России IX – начала XX в. М., 1991.

3. Крестьянские войны в России ХVII-ХVIII веков. М., 1974.

4. Орлов А.С., Георгиев В.А., Георгиева Н.Г., Сивохина Т.А. История России: Учебник. М., 2009. С. 98 – 116.

5. Орлов А.С. и др. Хрестоматия по истории России: Учеб. пособие. М., 2009. С. 147 – 158.

6. Платонов С.Ф. Учебник русской истории. СПб., 1994.

7. Сахаров А.М. Образование и развитие российского государства в ХIV-ХVII в. М., 1969.

8. Скрынников Р.Г. Крест и корона: Церковь и государство на Руси IХ-ХVII вв. СПб., 2000.

9. Талина Г.В. Царь Алексей Михайлович: личность, мыслитель, государственный деятель. М., 1996.

1. Виды систем уравнений

2. Проблема идентификации

3. Правила идентификации

4. Оценивание параметров структурной модели

5. Косвенный метод наименьших квадратов (КМНК)

6. Двухшаговый метод наименьших квадратов (ДМНК)

Не всегда получается описать адекватно сложное социально-экономическое явление с помощью только одного соотношения (уравнения). Кроме того, некоторые переменные могут оказывать взаимные воздействия и трудно однозначно определить какая из них является зависимой, а какая независимой переменной. Поэтому при построении эконометрической модели прибегают к системам уравнений.

В любой эконометрической модели в зависимости от конечных прикладных целей ее использования все участвующие в ней переменные подразделяются на:

1. Экзогенные (независимые) - значения которых задаются «извне», автономно, в определенной степени они являются управляемыми (планируемыми) ;

2. Эндогенные (зависимые) - значения которых определяются внутри модели, или взаимозависимые .

3. Лаговые - экзогенные или эндогенные переменные эконометрической модели, датированные предыдущими моментами времени и находящиеся в уравнении с текущими переменными. Например: - текущая эндогенная переменная, - лаговая эндогенная переменная (отстоящая от текущей на 1 период назад), - тоже лаговая эндогенная переменная (отстоя­щая от текущей на 2 периода).

4. Предопределенные переменные - переменные, опреде­ляемые вне модели. К ним относятся лаговые и текущие экзогенные переменные , а также лаговые эндогенные переменные .

Все эконометрические модели предназначены для объяснения текущих значений эндогенных переменных по значениям предопределенных переменных. Система уравнений в эконометрических исследованиях может быть построена по-разному. Выделяют следующие 3 вида систем уравнений.

1. Система независимых уравнений, когда каждая зависимая переменная рассматривается как функция только от предопределенных переменных :

2. Система рекурсивных уравнений, когда в каждом последующем уравнении системы зависимая переменная (y) представляет функцию от всех зависимых и предопределенных переменных предшествующих уравнений:

В рассмотренных 2-ух видах систем каждое уравнение может рассматриваться самостоятельно, и параметры урав­нения определяются с помощью метода наименьших квад­ратов (МНК).

3. Система взаимозависимых (совместных, одновременных) уравнений, когда одни и те же зависимые пере­менные в одних уравнениях входят в левую часть, а в других уравнениях - в правую часть системы (т.е. выступают в роли факторов):

Название «система одновременных уравнений» подчеркивает тот факт, что в системе одни и те же переменные одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других.

В эконометрике эта система уравнений также называется структурной формой модели.

В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим, т.к. нарушаются предпосылки, лежащие в основе МНК. В результате оценки получаются смещенными.

Некоторые из уравнений системы могут быть представлены в виде тождеств, т.е. параметры этих уравнений являются константами.

От структурной формы легко перейти к так называемой приведенной форме модели, в которой все эндогенные переменные выражены через предопределенные переменные:

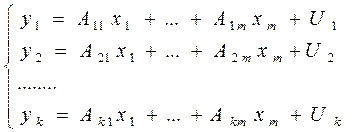
Особенность приведенной формы: так как правая часть каждого из уравнений модели содержит только пре­допределенные переменные и остатки, а левая часть только одну из эндогенных переменных, то такие системы относят к независимым. Тогда параметры каждого из уравнений системы в приведенной форме можно определить незави­симо обычным МНК.

Зная оценки этих коэффициентов можно определить параметры структурной формы модели (косвенный МНК).

Дата добавления: 2013-12-13