Оценивание параметров структурной модели

Коэффициенты структурной модели могут быть оценены раз­ными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:

• косвенный метод наименьших квадратов;

• двухшаговый метод наименьших квадратов;

• трехшаговый метод наименьших квадратов;

• метод максимального правдоподобия с полной информацией;

• метод максимального правдоподобия при ограниченной информации.

Косвенный и двухшаговый методы достаточно легкореализуемы. Косвенный метод наи­меньших квадратов (КМНК) применяется для идентифицируе­мой системы одновременных уравнений, а двухшаговый метод наименьших квадратов (ДМНК) используется для оценки коэф­фициентов сверхидентифицируемой модели. Перечисленные ме­тоды оценивания также используются для сверхидентифицируемых систем уравнений.

Метод максимального правдоподобия рассматривается как наиболее общий метод оценивания, результаты которого принормальном распределении признаков совпадают с МНК: Одна­ко при большом числе уравнений системы этот метод приводит к достаточно сложным вычислительным процедурам. Поэтому в качестве модификации используется метод максимального прав­доподобия при ограниченной информации (метод наименьшего дисперсионного отношения), разработанный в 1949 г. Т.Андер­соном и Н.Рубиным. В отличие от метода максимального правдоподобия в данном методе сняты ограничения на параметры, связанные с функционированием системы в целом. Это делает решение более про­стым, но трудоемкость вычислений остается достаточно высокой. Несмотря на его значительную популярность, к середине 60-х годов он был практически вытеснен двухшаговым методом наименьших квадратов (ДМНК) в связи с гораздо большей простотой последнего.

Дальнейшим развитием ДМНК является трехшаговый МНК (ТМНК), предложенный в 1962 г. А. Зельнером и Г. Тейлом. Этот метод оценивания пригоден для всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективным оказывается ДМНК.

Косвенный метод наименьших квадратов (КМНК)

Оценка точно идентифицированного уравнения осу­ществляется с помощью косвенного метода наименьших квадратов (КМНК).

Алгоритм КМНК включает 3 шага:

1) составление приведенной формы модели и выражение каждого коэффициента приведенной формы через структурные параметры;

2) применение обычного МНК к каждому уравнению приведенной формы и получение численных оценок приведенных параметров;

3) определение оценок параметров структурной формы по оценкам приведенных коэффициентов, используя соотношения, найденные на шаге 1.

При сравнении результатов, полученных традиционным МНК и с помощью КМНК, следует иметь в виду, что традиционный МНК, применяемый к каждому уравнению структурной формы модели, взятому в отдельности, дает смещенные оценки структурных коэффициентов.

Кроме того, при интерпретации коэффициентов множественной регрессии предполагается независимость факторов друг от друга, что становится невозможным при рассмотрении системы совместных уравнений.

Нарушение предпосылки независимости факторов друг от друга при использовании традиционного МНК в системе одновременных уравнений приводит к несостоятельности оценок структурных коэффициентов; в ряде случаев они оказываются экономически бессмысленными. Опасность таких результатов возрастает при увеличении числа эндогенных переменных в правой части системы, ибо становится невозможным расщепить совместное влияние эндогенных переменных и видеть изолированные меры их воздействия в соответствии с предпосылками традиционного МНК.

Двухшаговый метод наименьших квадратов (ДМНК)

Оценка сверхидентифицированного уравнения осуще­ствляется при помощи двухшагового метода наименьших квадратов.

Алгоритм ДМНК включает следующие шаги:

1) составление приведенной формы модели;

2) применение обычного МНК к каждому уравнению приведенной формы и получение численных оценок приве­денных параметров;

3) определение расчетных значений эндогенных пере­менных, которые фигурируют в качестве факторов в струк­турной форме модели;

4) определение структурных параметров каждого уравнения в отдельности обычным МНК, используя в каче­стве факторов входящие в это уравнение предопределенные переменные и расчетные (теоретические) значения эндогенных переменных, полученные на шаге 1.

Основная идея ДМНК — на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения.

Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название двухшагового МНК, ибо дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной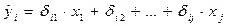и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.

Сверхидентифицируемая структурная модель может быть двух типов:

• все уравнения системы сверхидентифицируемы;

• система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.

Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения исполняется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.

ДМНК является наиболее общим и широко распространенным методом решения системы одновременных уравнений. Для точно идентифицируемых уравнений ДМНК дает тот же результат, что и КМНК.

Несмотря на важность системы эконометрических уравнений, на практике часто не принимают во внимание некоторые взаимосвязи, применение традиционного МНК к одному или нескольким уравнениям также широко распространено в эконометрике.

В частности, при построении производственных функций анализ спроса можно вести, используя обычный МНК.

Пример

Изучается модель вида

где у - валовой национальный доход;

- валовой национальный доход предшествующего года;

С - личное потребление;

D - конечный спрос (помимо личного потребления);

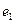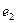, - случайные составляющие.

Информация за девять лет о приростах всех показателей дана в табл.1

Таблица 1

Год	D		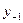y	C
	-6,8	46,7	3,1	7,4
	22,4	3,1	22,8	30,4
	-17,3	22,8	7,8	1,3
	12,0	7,8	21,4	8,7
	5,9	21,4	17,8	25,8
	44,7	17,8	37,2	8,6
	23,1	37,2	35,7	30,0
	51,2	35,7	46,6	31,4
	32,3	46,6	56,0	39,1
Сумма	167,5	239,1	248,4	182,7

Для данной модели была получена система приведенных урав­нений:

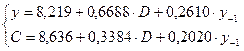
Требуется:

1. Провести идентификацию модели.

2. Рассчитать параметры первого уравнения структурной модели.

Решение

1. В данной модели две эндогенные переменные (у и С) и две экзо­генные переменные (D и 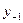). Второе уравнение точно идентифици­ровано, так как содержит две эндогенные

переменные и не содержит одну экзогенную переменную из системы. Иными словами, для вто­рого уравнения имеем по счетному правилу идентификации равен­ство: 2=1 + 1.

Первое уравнение сверхидентифицировано, так как в нем на па­раметры при С и D наложено ограничение: они должны быть равны. В этом уравнении содержится одна эндогенная переменная у. Пере­менная С в данном уравнении не рассматривается как эндогенная, так как она участвует в уравнении не самостоятельно, а вместе с пе­ременной D. В данном уравнении отсутствует одна экзогенная пере­менная, имеющаяся в системе. По счетному правилу идентификации получаем: 1 + 1 = 2: D + 1 > Н. Это больше, чем число эндогенных переменных в данном уравнении, следовательно, система сверх-идентифицирована.

2. Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов.

Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретиче­ские значения эндогенной переменной С. Для этого в приведенное уравнение

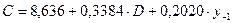
подставим значения D и 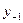, имеющиеся в условии задачи. Получим:

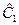= 15,8; = 16,8; 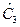= 7,4; = 14,3; = 15,0; 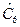= 27,4; = 24,0;

= 33,2; 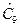= 29,0.

Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения С на теоретические 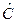и рассчитываем новую переменную 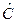+ D (табл. 2).

Таблица 2

Год	D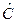
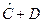
	-6,8	15,8	9,0
	22,4	16,8	39,2
	-17,3	7,4	-9,9
	12,0	14,3	26,3
	5,9	15,0	20,9
	44,7	27,4	72,1
	23,1	24,0	47,1
	51,2	33,2	84,4
	32,3	29,0	61,3
Сумма	167,5	182,7	350,2

Далее к сверхидентифицированному уравнению применяется метод наименьших квадратов. Обозначим новую переменную 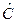+ D через Z. Решаем уравнение

.

Система нормальных уравнений составит:

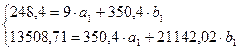
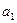= 7,678; 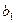= 0,512.

Итак, первое уравнение структурной модели будет таким:

у=7,678 + 0,512 (С + D).

Поскольку второе уравнение точно идентифицировано, то оценка его параметров может быть дана с помощью косвенного метода наименьших квадратов (КМНК).

Исходя из приведенной модели, выразим переменную D из первого уравнения системы и подставим во второе уравнение:

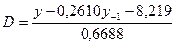
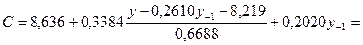
=8,636+0,506y-0,1321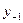-4,1587+0,2020=

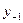=4,4773+0,506y+0,699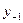

Это же уравнение C=4,4773+0,506y+0,699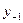можно получить, применяя ДМНК ко второму структурному уравнению. В этом случае сначала определяем 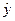из первого уравнения приведенной системы, подставляя в него значения D и 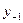, а затем используем МНК к уравнению .

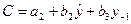При этом 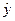составит:

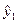=15,86; 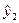=24,01; =2,60;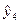=18,28; =17,75;

=42,76; =33,38; 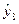=51,78; 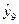=41,98; =248,4

что указывает на правильность расчетов, ибо 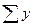==248,4.

Применяя МНК по второму структурному уравнению и используя при этом не фактические значения y, а расчетные, т.е. 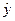, получим систему нормальных уравнений:

По данным примера получаем:

Откуда

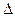=33391334; 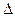a=149485264;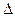 =16896029; 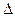=2334321;

a=4,4768; =0,506; =0,699

Соответственно второе структурное уравнение составит:

y=4, 4768+0,506y+0,699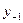

Как видим, результат совпадает с КМНК, но трудоемкость вычислений возросла.

Дата добавления: 2013-12-13