Графы и схемы

Изучаемые вопросы:

1. Понятие «граф».

2. Описание отношений.

3. Ориентированный граф.

4. Схема рассуждений.

Наглядное обучение, по словам К.Д.Ушинского, должно строиться на конкретных образах, непосредственно воспринятых ребенком. И в этом контексте процесс ознакомления младших школьников в курсе информатики с элементами теории графов является реализацией на практике наглядности как одного из ведущих дидактических принципов обучения. В младшей школе графы рассматриваются как разновидность рисунка, изображения, и естественным образом воспринимаются детьми, поскольку практически все учебные занятия в компьютерном классе так или иначе связаны с наглядно-образным представлением информационных объектов.

Пропедевтическим этапом ознакомления учащихся с понятием «граф» можно считать выполнение ими заданий на сопоставление объектов и их свойств (характеристик), например: осень — желтые листья, арбуз — полосатый (в целях наглядности дети соединяли линиями названия объектов и соответствующие признаки). По этим рисункам, говорит учитель, можно было ответить на вопрос: какой это предмет? Но в то же время каждый объект из чего-то состоит и это тоже можно нарисовать, например: мишка — туловище, голова, лапы, хвост и т.д. Все эти изображения — не что иное, как граф или объединение конечного числа объектов (объект обозначается точкой и называется «вершина») и линий — «ребер», которыми соединены объекты. После этого, пользуясь графами, представленными на доске, дети отвечают на вопросы: сколько вершин у графа? сколько ребер?

После этого учитель предъявляет граф более сложной структуры и поясняет, что обозначают в нем ребра (принадлежность, отношения между объектами или связи, например, кто с кем дружит в классе). Дети при помощи учителя коллективно решают, применяя граф-схемы, задачи комбинаторного типа. Например, в соревнованиях участвуют пятеро шахматистов. Каждый из них должен сыграть по одной партии с каждым. Сколько всего будет сыграно шахматных партий?

Дальнейшая логика изложения материала может быть такой. Когда мы собираемся куда-то пойти или поехать, для нас важно точно знать направление движения. То же самое справедливо и для графа, ведь от вершины к вершине можно перемещаться, двигаясь в различных направлениях. Существует специальное обозначение — линия со стрелкой, которая показывает направление движения или «путь» в графе, который будем называть ориентированным. Иллюстрацией сказанного может служить задание: «По заданному описанию нарисуй граф: утенок бросил мяч крольчонку, тот - котенку, котенок — гусенку, а гусенок — мышонку». И еще один момент, связанный с предыдущим материалом: при помощи ориентированного графа может быть описано логическое правило ЕСЛИ—ТО (следу­ет пояснить, что стрелка показывает путь от условия к заключению).

Необходимо объяснить детям, что для того чтобы правильно назвать путь, достаточно перечислить по порядку следования все вершины (это позволяет сравнивать пути между собой). Следует обратить особое внимание и подтвердить примером случай, когда между вершинами нет пути, а также пояснить, что путей между одними и теми же вершинами бывает несколько. В целях закрепления — предложить практические задания на заполнение «пустых» вершин графа и описание путей между конкретными вершинами.

Очень важное умение строить схемы по высказываниям с логическими операциями И, ИЛИ и на этой основе делать правильные выводы (рис. 1).

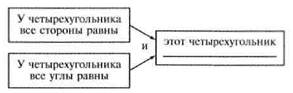
Рис. 1. Схема рассуждений

На заключительном этапе, формулируя несколько вариантов возможных выводов, учитель может попросить учащихся определить, какой из этих выводов единственно верный (оценить с точки зрения истинности), а также построить схему состава по изображению или рассказу (тексту).

В результате обучения учащиеся должны:

· знать (понимать): понятия «граф», «вершина», «ребро», «путь»;

· уметь: строить графы по словесному описанию отношений между объектами; выбирать граф, правильно изображающий предложенную ситуацию;

· использовать приобретенные знания и умения в практической деятельности и повседневной жизни: для расширения кругозора в областях знании, связанных с информатикой: алгебра логики, теория графов, комбинаторика.

Построение схем и графов знакомит младших школьников с одним из способов решения задач, учит структурировать информацию, планировать действия, эффективно вести поиск информации, служит пропедевтикой графического способа описания информационных моделей, иерархического способа представления файловой системы.

Дата добавления: 2013-12-13