Играет роль аргумента этой функции, т.е

Таким образом,

Р{у = 1/х}= F(b₀+b₁х₁+...b_m-1x_m-1),

где, F-это функция распределения случайной величины ( - e)

Во многих экономических задачах, скрытую переменную вводят сразу, считая, что:

Отметим, что случайные величины e_i предполагаются независимыми друг от друга, а также независимыми от х_i.

Описывать вероятность непосредственно линейной функцией (то есть, выбирать в качестве F-линейную функцию), нецелесообразно, так как в этом случае значения предсказанной (вычисленной по модели) вероятности могут быть как отрицательными, так и превосходящими единицу. Вместо этого для моделирования значений

Р{у = 1|Х}

подбирают функции, область значений которых определяется отрезком [0,1], а линейная функция

z=b₀+b₁х₁+...b_m-1x_m-1

Р{у =1|Х} = F(b₀+b₁х₁+...b_m-1x_m-1) = F(z)

(4.6.1)

причем функции F(z)(какую бы мы не выбрали!!!) должны удовлетворять следующим требованием

(4.6.2)

График одной из функций данного вида приведен на рисунке:

.

Модели рассмотренного типа для оценивания вероятности указанного события называют обычно моделями бинарного выбора. Наиболее распространенными моделями бинарного выбора являются так называемые логит- и пробит-модели.

ОПРЕДЕЛЕНИЕ 4.6.1. Логит-модель. Модель вида (4.6.1) при условиях (4.6.2) для функции F(z), называется логит -моделью, если в качестве F(z) рассматривается логистическая функция, т. е.

(4.6.3)

Нетрудно проверить, что эта функция удовлетворяет условиям (4.6.2), ее часто обозначают через Λ(z).

ОПРЕДЕЛЕНИЕ.4.1.2 Пробит-модель. Модель вида (4.6.1) называется пробит -моделью, если в качестве F(z) рассматривается функция распределения стандартного нормального распределения, т.е.

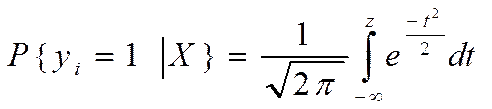
(4.6.4)

Так же, как и функция Λ(z), нормальная функция распределения F(z) удовлетворяет всем условиям (4.6.2) и является симметричной относительно z = 0.

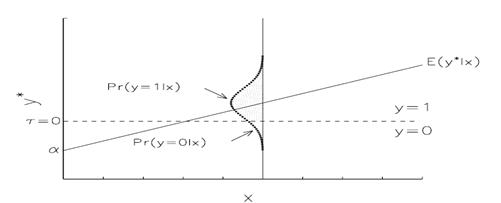
Figure 4.1: Relationship between latent variable y∗ and Pr(y = 1) for the BRM.

Рисунок заимствован из книги «REGRESSION MODELS FORCATEGORICAL DEPENDENT VARIABLES USING STATA»

Дата добавления: 2013-12-13