В подобных ситуациях вектор

В этой главе мы рассмотрим, в частности, эконометрические модели, которые используют в том случае, когда ЗАВИСИМАЯ переменная измерена в номинальной или порядковой шкале.

Номинальной шкале.

Порядковой шкале.

Метрической шкале (являться количественными).

Логит- и пробит-модели

Как мы уже обсуждали, в эконометрическом моделировании работают с переменными, которые могут быть измерены в:

Предположим, что результирующий показатель у, «поведение» которого существенно зависит от количественных объясняющих переменных (матрица Х)

Х = (1, х₁, ,...,х_m-1),

является качественной переменной, определяющей одно из двух возможных состояний характеризуемого ею объекта, то есть переменной измеренной в номинальной шкале (в общем случае этих состояний может быть больше). Например, результирующему показателю

y_i может быть приписано значение равное 0, если i -й индивидуум оказался безработным в обследуемом периоде времени, и 1 — в противном случае.

То есть:

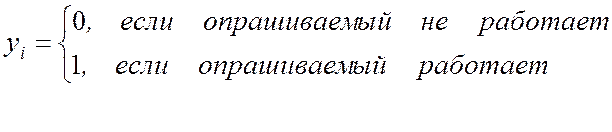
Y = (у₁, y₂,…,y_n) ^T

исходных статистических данных зависимой переменной будет состоять только из: «0» или «1

Можно ли построить линейную регрессионную модель, описывающую зависимость у от хв данном случае?

Ответ: вряд ли. Неясно, как интерпретировать в этом случае оцененные при помощи регрессии значения у, которые будут уже измерены в метрическойнепрерывной (количественной) шкале и могут принимать различные значения.

Поэтому для исследования статистической связи между у и_Хстроят некоторую специальную регрессионную модель зависимости вероятности

Р{у = 1|Х}

от линейной функции наблюдаемых факторов.

Модель бинарного выбора обосновывают при помощи скрытой (латентной) переменной. Например, предположим, что мы изучаем информацию о том, какое решение принимает замужняя женщина: работать ей, или нет. Считают, что ее потребительское и трудовое поведение описывается некоторой функцией полезности. Эта функция зависит от многих характеристик: дохода, свободного времени, наличия детей, образования. Женщина может принять решение выйти на работу, чтобы увеличить доход семьи, но при этом произойдет уменьшение времени, уделяемого детям, домашней работе и т.п. Или, она может принять решение не работать. Каждой из рассмотренных ситуаций, соответствует своя величина функции полезности. Предположим, что 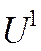это величина полезности, если женщина работает, а 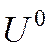- величина полезности, если женщина не работает.

Если

>,

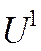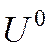то женщине выгоднее пойти работать, так как получаемый дополнительный доход перевешивает уменьшение времени на детей и домашние дела.

Если

<,

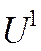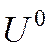то женщина не выходит на работу.

Обозначим разность

-=

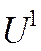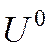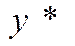
и предположим, что эта величина является линейной функцией от наблюдаемых характеристик х_i: величины заработной платы, возраста, наличия детей и т.д.

Предположим, что

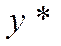=b₀+b₁х₁+...b_m-1x_{m- 1} +e

Тогда

Р{у = 1}= Р{у*³0}=

= Р{b₀+b₁х₁+...b_m-1x_m-1 +e ³0}=

= Р{e ³- (b₀+b₁х₁+...b_m-1x_m-1)}=

Р{-e <b₀+b₁х₁+...b_m-1x_m-1}=

=F(b₀+b₁х₁+...b_m-1x_m-1).

Дата добавления: 2013-12-13