
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предмет, задачи и методы организационной психологии. Лекция № 18. Задачи, приводящие к понятию производной
|
|
|
|
Вводная часть
Лекция № 18. Задачи, приводящие к понятию производной. Определение производной. Дифференцируемость функции. Связь между непрерывностью и дифференцируемостью функций. Производные некоторых основных элементарных функций.
Лекция № 17. Некоторые пределы, связанные с показательной и логарифмической функциями. Точки разрыва и их классификация. Свойства функций, непрерывных на отрезке.
Теорема 1.  .
.
Доказательство.  .
.
Замечание. В частности, если  , то имеем
, то имеем  .
.
Теорема 2. 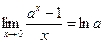 .
.
Доказательство. Пусть  . Тогда
. Тогда  . Если
. Если 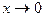 , то
, то  . Поэтому
. Поэтому  .
.
Замечание. В частности, если  , то имеем
, то имеем 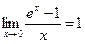 .
.
Теорема 3. 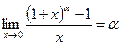 .
.
Доказательство. Пусть  . Тогда
. Тогда 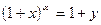 или
или  . Если
. Если 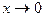 , то
, то  . Поэтому получаем
. Поэтому получаем 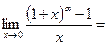
 .
.
Таким образом установлена эквивалентность следующих бесконечно малых функций при 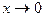 :
:  ~
~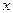 ;
; 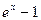 ~
~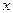 ;
; 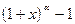 ~
~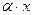 .
.
Если функция 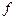 не является непрерывной в точке
не является непрерывной в точке  , то ее называют разрывной в этой точке, а точку
, то ее называют разрывной в этой точке, а точку  - точкой разрыва. Функция
- точкой разрыва. Функция 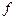 может иметь разрыв в точке
может иметь разрыв в точке  в следующих случаях:
в следующих случаях:
1) не существует  ;
;
2)  существует, но
существует, но 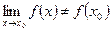 .
.
3) функция 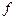 неопределена в точке
неопределена в точке  , но определена в некоторой проколотой окрестности этой точки.
, но определена в некоторой проколотой окрестности этой точки.
Пусть  - точка разрыва функции
- точка разрыва функции 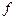 . Ее называют точкой разрыва первого рода, если существуют конечные односторонние пределы функции
. Ее называют точкой разрыва первого рода, если существуют конечные односторонние пределы функции 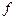 в точке
в точке  . В противном случае (т.е. когда хотя бы один из односторонних пределов не существует или бесконечен) точка
. В противном случае (т.е. когда хотя бы один из односторонних пределов не существует или бесконечен) точка  называется точкой разрыва второго рода. В свою очередь разрыв первого рода может быть устранимым, если
называется точкой разрыва второго рода. В свою очередь разрыв первого рода может быть устранимым, если  и неустранимым, если
и неустранимым, если  . В случае неустранимого разрыва разность
. В случае неустранимого разрыва разность 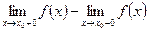 называется скачком.
называется скачком.
Основные свойства функций, непрерывных на отрезке, выражаются двумя теоремами Вейерштрасса и двумя теоремами Больцано-Коши.
1 Теорема Вейерштрасса. Если функция 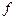 определена и непрерывна на отрезке
определена и непрерывна на отрезке 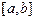 , то она ограничена.
, то она ограничена.
2 Теорема Вейерштрасса. Если функция 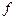 непрерывна на отрезке
непрерывна на отрезке 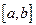 , то среди всех ее значений есть наибольшее и наименьшее.
, то среди всех ее значений есть наибольшее и наименьшее.
1 Теорема Больцано-Коши. Если функция 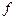 непрерывна на отрезке
непрерывна на отрезке 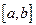 и на концах его принимает значения разных знаков, то внутри
и на концах его принимает значения разных знаков, то внутри 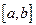 найдется точка
найдется точка 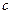 такая, что
такая, что  .
.
2 теорема Больцано-Коши. Если функция 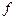 непрерывна на отрезке
непрерывна на отрезке 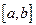 и
и 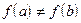 , то для любого числа
, то для любого числа 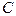 между
между  и
и 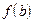 найдется точка
найдется точка 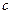 из
из 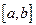 такая, что
такая, что 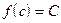 .
.
Следствие. Если функция 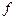 непрерывна на
непрерывна на 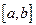 , то множество значений этой функции является отрезком.
, то множество значений этой функции является отрезком.
Рассмотрим кривую, заданную уравнением  , где
, где 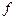 - непрерывная функция. Пусть
- непрерывная функция. Пусть  - некоторая точка этой кривой. Для определения касательной в точке
- некоторая точка этой кривой. Для определения касательной в точке 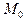 выберем на кривой произвольно точку
выберем на кривой произвольно точку 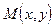 и проведем секущую
и проведем секущую  . (рис.3) Ясно, что если перемещать точку
. (рис.3) Ясно, что если перемещать точку 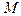 по кривой, то положение секущей
по кривой, то положение секущей  будет меняться. Причем, при движении точки
будет меняться. Причем, при движении точки 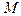 к
к 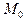 эта секущая будет стремиться к некоторому предельному положению, которое займет, когда
эта секущая будет стремиться к некоторому предельному положению, которое займет, когда 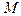 совпадет с
совпадет с 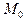 .
.
Предельное положение секущей  , когда точка
, когда точка 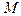 стремится к точке
стремится к точке 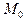 по любому закону, перемещаясь по кривой, называется касательной к кривой
по любому закону, перемещаясь по кривой, называется касательной к кривой  в точке
в точке  .
.
Теперь приступим к решению задачи. Будем считать, что нам даны кривая  и точка
и точка  на этой кривой. Уравнение касательной будем искать в виде
на этой кривой. Уравнение касательной будем искать в виде 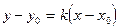 , где
, где 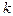 - угловой коэффициент касательной. Для решения задачи достаточно найти
- угловой коэффициент касательной. Для решения задачи достаточно найти 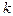 . Из рисунка видно, что угловой коэффициент секущей
. Из рисунка видно, что угловой коэффициент секущей  находится как
находится как  . Если точку
. Если точку 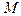 устремить к точке
устремить к точке 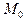 (при этом
(при этом 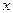 устремится к
устремится к  ), то угловой коэффициент секущей устремится к угловому коэффициенту касательной, т.е.
), то угловой коэффициент секущей устремится к угловому коэффициенту касательной, т.е.
 (1)
(1)
Определив угловой коэффициент касательной по формуле (1), завершаем решение задачи.
Задача 2 (о мгновенной скорости). Пусть точка 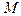 движется по прямой и
движется по прямой и
известен закон ее движения, заданный функцией 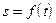 . Найти
. Найти
скорость движения точки в момент  .
.
Решение. Зная время 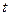 движения точки, можно найти путь, пройденный точкой
движения точки, можно найти путь, пройденный точкой 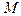 от начала движения до момента
от начала движения до момента 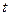 . Этот путь равен
. Этот путь равен  . Значит путь, пройденный точкой
. Значит путь, пройденный точкой 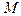 от начала движения до момента
от начала движения до момента  , равен
, равен 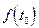 . Поэтому за время
. Поэтому за время 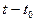 точка
точка 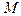 пройдет путь
пройдет путь  . Средняя скорость движения точки от момента
. Средняя скорость движения точки от момента  до момента
до момента 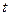 равна
равна 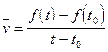 . Скорость движения точки в момент
. Скорость движения точки в момент  может быть найдена как
может быть найдена как  . Итак
. Итак  , т.е. получили тот же предел (1), что и в задаче о касательной.
, т.е. получили тот же предел (1), что и в задаче о касательной.
Итак мы рассмотрели две совершенно различные по содержанию задачи. Однако решение обеих задач свелось к одной и той же математической операции - вычислению предела (1). Это говорит о большой значимости полученного предела.
Пусть функция 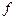 определена в некоторой окрестности точки
определена в некоторой окрестности точки  .
.
Определение 1. Если существует конечный предел 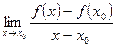 ,
,
то его называют производной от функции 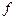 в точке
в точке 
и обозначают символом 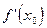 , или
, или 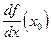 .
.
Таким образом 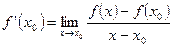 . Заметим, что этот предел можно записать в другом виде. Обозначим
. Заметим, что этот предел можно записать в другом виде. Обозначим 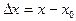 . Отсюда
. Отсюда 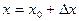 . Поэтому
. Поэтому  .
.
Если теперь вернуться к рассмотренным задачам, то увидим, что угловой коэффициент касательной к кривой  в точке
в точке  есть производная от функции
есть производная от функции 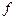 в точке
в точке  . В этом состоит геометрический смысл производной. С другой стороны, мгновенная скорость точки
. В этом состоит геометрический смысл производной. С другой стороны, мгновенная скорость точки  есть производная от функции
есть производная от функции 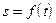 , выражающей зависимость пути от времени, в точке
, выражающей зависимость пути от времени, в точке  . В этом состоит механический смысл производной.
. В этом состоит механический смысл производной.
Если предел в определении 1 будет бесконечным или односторонним,
то производную называют соответственно бесконечной или односторонней.
Правостороннюю производную обозначают символом  , а левостороннюю – символом
, а левостороннюю – символом  .
.
Очевидно, что для существования конечной производной в точке  необходимо и достаточно, чтобы существовали обе односторонние производные и чтобы
необходимо и достаточно, чтобы существовали обе односторонние производные и чтобы 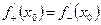 .
.
Определение 2. Функция 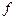 называется дифференцируемой в точке
называется дифференцируемой в точке  , если ее
, если ее
приращение в точке  может быть представлено в виде
может быть представлено в виде
 , (*)
, (*)
где 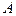 - некоторое число, a
- некоторое число, a  - бесконечно малая
- бесконечно малая
функция при  .
.
Теорема 1. Чтобы функция 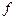 была дифференцируема в точке
была дифференцируема в точке  , необходимо и
, необходимо и
достаточно чтобы функция 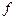 имела конечную производную в точке
имела конечную производную в точке
 .
.
Следствие. Если функция 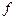 дифференцируема в точке
дифференцируема в точке  , то она непрерывна в
, то она непрерывна в
точке  .
.
Замечание 1. Утверждение, обратное утверждению следствия, неверно.
Замечание 2. При доказательстве теоремы 1 был установлен факт, что если
имеет место равенство (*), то в нем  Поэтому
Поэтому
равенство (*) можно записывать в виде
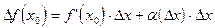
Рассмотрим нахождение производных некоторых основных элементарных функций.
1)  Найдем
Найдем 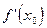 .
.
 .
.
2) 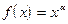 .Найдем
.Найдем 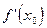 .
.

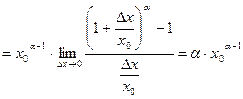
3) 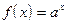 . Найдем
. Найдем 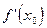 .
.
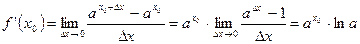 .
.
В частности, если  ,то имеем
,то имеем  .
.
4). 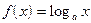 . Найдем
. Найдем 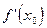 .
.
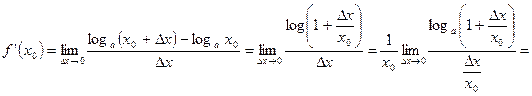
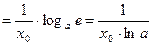 .
.
В частности, если  , то
, то  .
.
5) 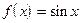 . Найдем
. Найдем 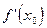 .
.

 .
.
6) 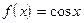 . Найдем
. Найдем 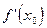 .
.
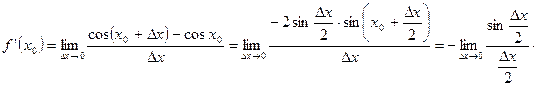
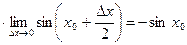
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 548; Нарушение авторских прав?; Мы поможем в написании вашей работы!