Эластичность. Экономическая интерпретация параметров МПФ. Норма замещения производственных факторов

Неоклассическая ПФ. Условия, которым должна отвечать неоклассическая ПФ и их экономическая интерпретация

ПФ (1.1) называется неоклассической, если она задана при всех неотрицательных значениях K и L и является непрерывной и нужное число раз дифференцируемой функцией своих аргументов и удовлетворяет следующим условиям, имеющим под собой экономическое обоснование.

1. Производство невозможно при отсутствии хотя бы одного ресурса:

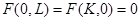. (1.5)

Это означает, что каждый из ресурсов необходим хотя бы в малых количествах. Заметим, что это условие выполняется для функции (1.2) и (1.3).

2. При увеличении затрат производственных ресурсов выпуск продукции растет. В математической форме, если ПФ дифференцируема это имеет вид:

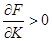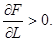, (1.6)

Так как 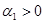и 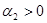, то согласно (1.6) МПФ обладает свойством 2, адекватным реальной экономике: с ростом затрат ресурсов выпуск растет.

3. По мере увеличения количества одного ресурса при постоянных количествах других скорость роста выпуска замедляется. Математически это требование для дважды дифференцируемых ПФ (1.1) выглядит так:

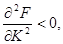
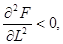(1.7)

Легко проверить, что для ПФ (1.2) это условие выполняется. Часто вместо (1.7) формулируется более сильное математическое требование: F(K,L) – вогнутая функция, т. е. для любых двух неотрицательных точек (K1, L1) и (K2, L2) и любого числа λ∈[0, 1] справедливо неравенство

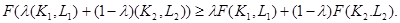(1.8)

Если функция F(K, L) дважды непрерывно дифференцируема, условие вогнутости эквивалентно требованию неположительной определенности матрицы вторых производных функции F(K, L) при всех положительных значениях вектора ресурсов (K, L), т. е.

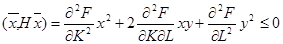
для всех векторов (x, y), где H матрица

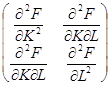(1.10)

Матрица Н называется матрицей Гессе (или гессианом).

4. При неограниченном увеличении одного из ресурсов выпуск неограниченно растет:

F(+ ∞, L) = F(K, + ∞) = + ∞. (1.11)

Из (1.2) также видно, что МПФ обладает свойством 4. Следовательно, ПФ (1.2) при 0< α₁< 1, 0< α₂< 1 является неоклассической.

Введем понятие эластичности как логарифмической производной факторов

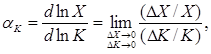
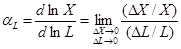(1.12)

Для мультипликативной ПФ 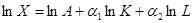и

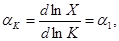
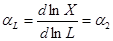. (1.13)

т.е. 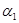– эластичность выпуска по ОПФ, – эластичность выпуска по труду. Из (1.12) видно, что коэффициент эластичности фактора показывает, на сколько процентов изменится выпуск, если фактор увеличится на 1%. В качестве примера приведем МПФ ВВ РФ (млрд. руб.) в зависимости от стоимости ОПФ (млрд. руб.) и числа занятых в народном хозяйстве (млн. чел.) по данным РФ за 1960-1994 гг. в ценах для этого периода

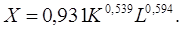
При увеличении ОПФ на 1%, ВВ увеличится на 0,539%, а при увеличении занятых на 1% – на 0,594%. Если 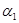> , то имеет место трудосберегающий (интенсивный) рост, в противном случае фондосберегающий (экстенсивный) рост. Параметр А интерпретируется как параметр технического прогресса: при тех же 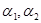выпуск в точке (K, L) больше, чем больше А.

Дата добавления: 2013-12-13