
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Повторные пределы
|
|
|
|
Следствие.
Монотонная на интервале 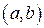 функция
функция 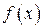 имеет конечный предел как справа, так и слева в каждой внутренней точке этого интервала.
имеет конечный предел как справа, так и слева в каждой внутренней точке этого интервала.
Доказательство.
Пусть функция не убывает на 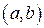 . Тогда для
. Тогда для 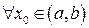 будем иметь:
будем иметь:
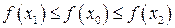 , где т.
, где т. 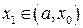 , т.
, т. 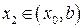 - произвольные точки из указанных промежутков. Согласно доказанной теореме
- произвольные точки из указанных промежутков. Согласно доказанной теореме  ,
, 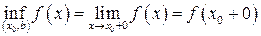 , причем
, причем
 , т.е.
, т.е.  и
и 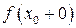 конечны.
конечны.
В данном параграфе рассмотрим числовую функцию векторного аргумента или функцию многих переменных:
 .
.
Для таких функций наряду с введенным ранее понятием предела 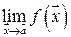 (при одновременном стремлении всех аргументов к их предельным значениям) могут существовать пределы другого рода, получаемые в результате ряда последовательных предельных переходов по каждому аргументу в отдельности в том или ином порядке. Пределы такого рода будем называть повторными.
(при одновременном стремлении всех аргументов к их предельным значениям) могут существовать пределы другого рода, получаемые в результате ряда последовательных предельных переходов по каждому аргументу в отдельности в том или ином порядке. Пределы такого рода будем называть повторными.
Рассмотрим функцию 2-х переменных 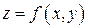 . Пусть эта функция определена в некоторой прямоугольной окрестности точки
. Пусть эта функция определена в некоторой прямоугольной окрестности точки  :
: 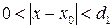 ,
, 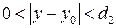 за исключением, может быть, самой этой точки. Если при всяком фиксированном
за исключением, может быть, самой этой точки. Если при всяком фиксированном 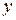 из промежутка
из промежутка 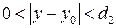 существует конечный предел
существует конечный предел  и, кроме того существует
и, кроме того существует 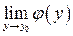 , то такой предел называется повторным пределом и обозначается
, то такой предел называется повторным пределом и обозначается  . Аналогично определяется повторный предел
. Аналогично определяется повторный предел  .
.
Примеры.
1)  . Не существует
. Не существует 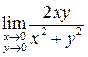 , что легко устанавливается с использованием определения Гейне:
, что легко устанавливается с использованием определения Гейне:
 ,
, 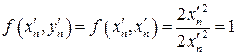 ;
;
 ,
,  .
.
Повторные пределы существуют и равны: 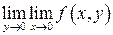 =
= =0.
=0.
2) 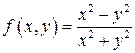 . Не существует
. Не существует 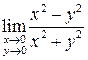 − доказывается по определению Гейне. Достаточно взять
− доказывается по определению Гейне. Достаточно взять 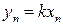 , где
, где 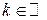 , тогда
, тогда  и
и 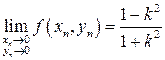 зависит от значения
зависит от значения 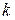 .
.
Повторные пределы существуют, но не равны между собой:
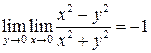 ,
, 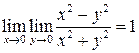 .
.
3) 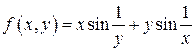 .
.  по леммам о бесконечно малых (
по леммам о бесконечно малых ( - б.м. при
- б.м. при 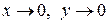 , а
, а  - ограниченные функции). Однако повторные пределы не существуют, ибо не существуют
- ограниченные функции). Однако повторные пределы не существуют, ибо не существуют 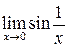 ,
,  .
.
Эти примеры показывают, что повторные пределы не всегда равны, а поэтому не всегда возможна перестановка предельных переходов. Для обоснования этой возможности рассмотрим теорему.
Теорема. Если 1) существует 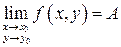 (
(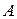 - конечное или
- конечное или 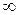 ); 2) при
); 2) при 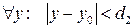 существует конечный
существует конечный  ;
;
то существует повторный предел, равный двойному:
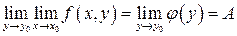 .
.
Доказательство.
Пусть 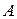 – конечно. Согласно определению Коши предела функции для
– конечно. Согласно определению Коши предела функции для  такое, что для
такое, что для 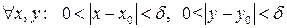
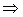
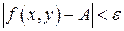
 .
.
Фиксируем 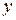 из проколотой
из проколотой  -окрестности
-окрестности 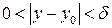 и в неравенстве
и в неравенстве  переходим к пределу при
переходим к пределу при 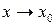 :
:  (используем условие 2) данной теоремы и теорему о предельном переходе в неравенстве). Согласно определению предела по Коши
(используем условие 2) данной теоремы и теорему о предельном переходе в неравенстве). Согласно определению предела по Коши 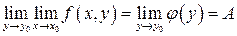 .
.
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 592; Нарушение авторских прав?; Мы поможем в написании вашей работы!