
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства непрерывных функций
|
|
|
|
Все степенные, показательные, логарифмические, тригонометрические и обратные тригонометрические функции непрерывны в областях существования.
1) Сумма непрерывных функций – есть непрерывная функция.
Действительно, из определения 1 непрерывности следует, что если 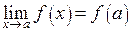 и
и 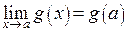 , то
, то
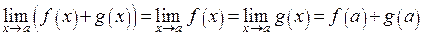 .
.
2). Произведение непрерывных функций есть функция непрерывная.
3). Частное непрерывных функций – функция непрерывная, если знаменатель в предельной точке не равен нулю.
Доказательства второго и третьего свойств также следует из свойств пределов.
4). Пусть функция 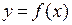 непрерывна в точке
непрерывна в точке 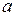 , пусть функция
, пусть функция  непрерывна в точке
непрерывна в точке 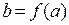 . Тогда функция
. Тогда функция 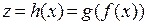 непрерывна в точке
непрерывна в точке 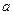 .
.
Очевидно, что 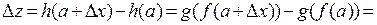
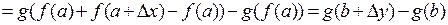 .
.
Так как согласно определению 3 непрерывности 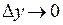 при
при 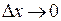 и
и 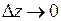 при
при 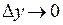 , получим:
, получим: 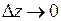 при
при 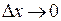 .
.
Таким образом, непрерывная функция от непрерывной функции есть функция непрерывная.
Пример. Функция 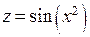 непрерывна во всех точках числовой оси, так как функция
непрерывна во всех точках числовой оси, так как функция 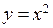 непрерывна на
непрерывна на 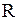 , а функция
, а функция 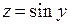 непрерывна на множестве неотрицательных чисел.
непрерывна на множестве неотрицательных чисел.
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 292; Нарушение авторских прав?; Мы поможем в написании вашей работы!