Формула Тейлора

Примеры.

Производные и дифференциалы высших порядков

Логарифмическое» дифференцирование

Здесь имеется ввиду дифференцирование с предварительным логарифмированием функции. Пусть . При вычислении производной нет возможности использовать таблицу производных, так как эта функция не является ни степенной, ни показательной. Прологарифмируем обе части уравнения 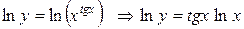. В результате от явного задания функции перешли к неявному, при этом функция стала более удобной для дифференцирования. В самом деле 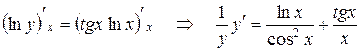. В результате

.

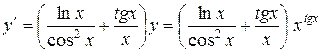Определение. Второй производной функции 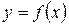называется производная ее первой производной .

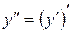Если физический смысл первой производной – есть скорость изменения функции, то вторая производная определяет скорость изменения скорости изменения функции, то есть ускорение.

1) Если 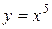, то 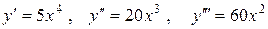и так далее.

2) Если 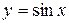, то

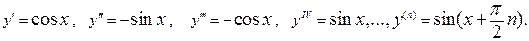
Аналогично определяются дифференциалы высших порядков. Дифференциал второго порядка – это дифференциал от дифференциала, т.к. 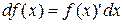, тогда

,

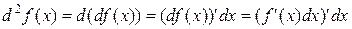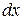- бесконечно малое приращение, не зависящее от x, поэтому производная от него считается как от постоянной. Т.е.

.

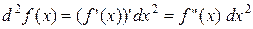Подобным образом получим .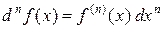

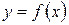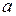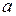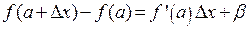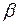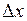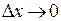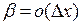Предположим, что функция имеет производную первого порядка в точке . Из определения дифференцируемости функции в точке имеем , где – бесконечно малая функция более высокого порядка, чем при (). Поэтому для точек 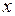, близких к точке 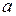справедлива формула

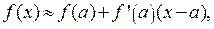
обеспечивающая первое приближение функции. Эта формула позволяет получать очень грубые приближенные значения функций в точках, так как ее можно трактовать как замену функции 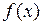многочленом первой степени в окрестности той точки 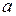, где значение функции и ее производной легко найти. Очевидно, что формула эта применима в очень малой окрестности точки .

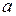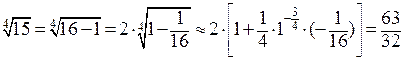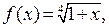
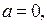
Пример. . Здесь мы использовали формулу первого приближения при 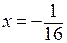. Поэтому 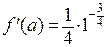и .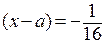

Возникают вопросы: 1) нельзя ли использовать многочлены более высоких степеней для более точного приближения функции? 2) как оценить ошибку приближения?

Формула Тейлора дает ответы на эти вопросы.

Предположим, что функция 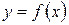имеет все производные до 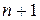порядка в некотором промежутке, содержащем точку a. В таком случае для всех значений 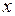из этого промежутка справедлива формула

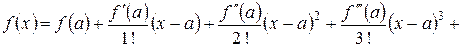
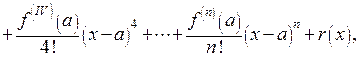
где остаточный член 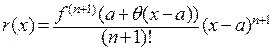и .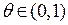

Таким образом, функция приближается многочленом, и ошибка вычислений, обусловленная заменой значения функции значением многочлена, равна остаточному члену. Поскольку точное значение 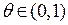не может быть найдено, значения функций вычисляются приближенно, и остаточный член служит не для подсчета, а для оценки ошибки. Последняя формула является обобщением формулы конечных приращений Лагранжа.

Следующий пример демонстрирует, как приближается функция 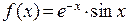(голубая линия) многочленами по формуле Тейлора (красная линия) в окрестности точки 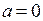при увеличении степеней многочленов от первой до одиннадцатой.

Taylor.wxm

Формулу Тейлора можно записать через дифференциалы:

.

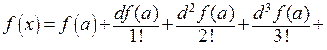
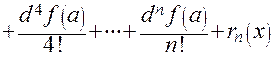Для приложений к вычислению пределов используют локальную формулу Тейлора, имеющую вид

.

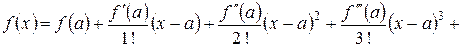
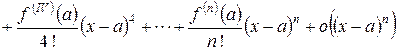Такое представление остаточного члена показывает, что остаточный член есть бесконечно малая более высокого порядка малости, чем .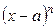

Локальная формула Тейлора является обобщением формулы связи приращения функции и дифференциала функции в точке.

В частности, при 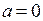формула Тейлора называется формулой Маклорена:

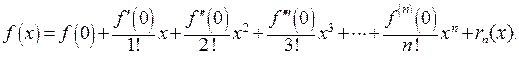
Примеры разложений элементарных функций по формуле Маклорена.

Пример 1. Рассмотрим функцию 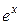. Нетрудно заметить, что любая производная этой функции равна самой функции, а 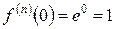. В соответствии с формулой Маклорена

.

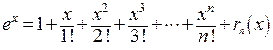Пример 2. Рассмотрим функцию 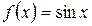. Так как 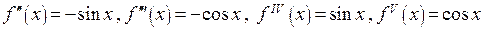и т.д., получим

….

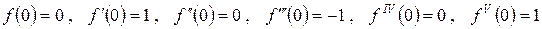Первые члены формулы Маклорена принимают вид

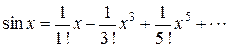
Анализируя первые члены разложения, записываем его общий член 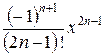. В результате

.

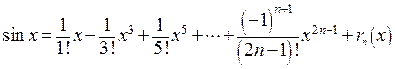Пример 3. Получим разложение по формуле Маклорена функции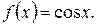

, .

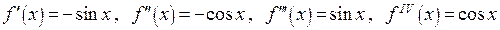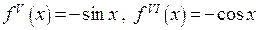Очевидно, что

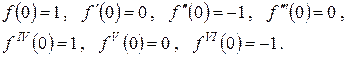
В соответствии с формулой Маклорена получаем

.

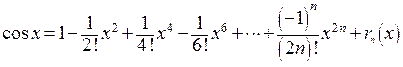Пример 4. Получим разложение по формуле Маклорена функции 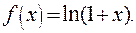Поскольку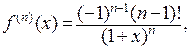 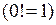, имеем 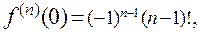поэтому получим разложение

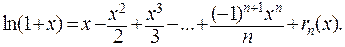
Это разложение может применяться только для значений x, для которых

Пример 5. Получим разложение по формуле Маклорена функции 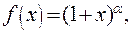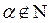. Дифференцируя, найдем

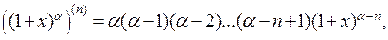
поэтому 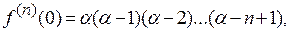и имеем разложение

.

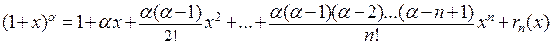Это разложение может применяться только для значений x, для которых

Дата добавления: 2013-12-13