Ряды с положительными членами

Рассмотрим числовой ряд ,

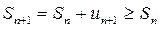где для такого ряда . Значит, последовательность частичных сумм возрастает.

Из теоремы о пределе монотонной последовательности можно сформулировать условие сходимости ряда с положительными членами.

Ряд с положительными членами всегда имеет сумму и эта сумма конечна, а ряд будет сходящимся, если частичные суммы ряда ограничены сверху, и бесконечна, а ряд расходящимся в противном случае.

Теоремы сравнения положительных рядов.

Пусть даны два положительных ряда:

и .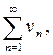

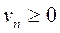Теорема 1. Если выполняется неравенство: , начиная с некоторого n, то из сходимости ряда второго (большего) ряда - следует сходимость первого (меньшего) ряда. А из расходимости ряда меньшего ряда следует расходимость ряда большего.

Доказательство:

Так как отбрасывание конечного числа начальных членов ряда не влияет на сходимость, можно считать, что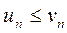

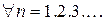
Для частичных сумм этих рядов выполняется

Пусть ряд сходится, тогда 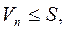и тем более 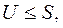значит ряд 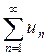- сходится.

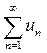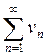Пусть расходится, тогда , значит и ряд расходится.

Теорема 2. Если существует конечный предел отношения общих членов двух рядов 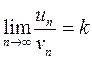, , 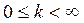то оба ряда сходятся или расходятся одновременно.

Примеры. Исследуйте на сходимость следующие ряды

1) 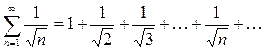сравним члены этого ряда с членами расходящегося гармонического ряда 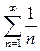, так как 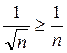, исследуемый ряд расходится.

2) Ряд сходится по теореме сравнения, так как предел отношения общего члена данного ряда к общему члену сходящегося (доказанный ранее) ряда 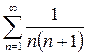есть 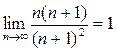, постоянное число.

3)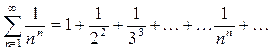Сравним этот ряд с рядом 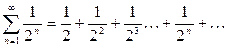, который представляет собой бесконечно убывающую геометрическую прогрессию со знаменателем 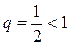, следовательно, сходится.

Так как 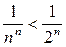исследуемый ряд сходится.

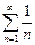4) Ряд сравним с рядом , который является расходящимся рядом. 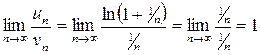с учетом того, что .

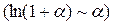Приведем полученные о сходимости некоторых рядов, которые могут быть использованы для сравнения:

1.

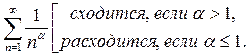
2.

3.

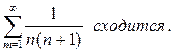
4.

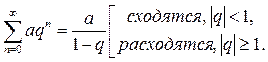
Достаточные признаки сходимости числовых рядов с положительными членами.

Признак Даламбера.

Теорема. Рассмотрим ряд 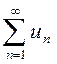с положительными членами и предел отношения последующего члена ряда к предыдущему.

1) Если 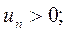2) существует 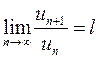, тогда

Доказательство:

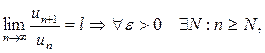
то есть .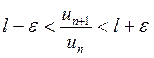

Рассмотрим 3 случая:

1) Выберем 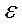столь малым, чтобы значение тогда, полагая , при значении 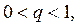имеем 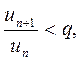для .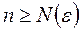

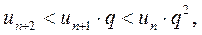
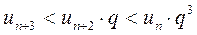и так далее.

Члены ряда меньше членов геометрической прогрессии: Так как 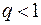, то ряд (2) сходится, значит, по теореме сравнения сходится и ряд (1).

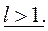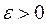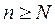
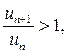
2) Возьмем столь малым, что тогда при члены ряда не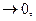не выполняется необходимый признак сходимости 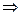ряд расходится.

3) 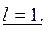Покажем, что в этом случае ряд может как сходиться, так и расходиться.

1) гармонический ряд 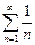расходится, для него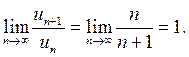

2) Рассмотрим ряд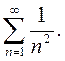

Для него Сравним члены исследуемого ряда со сходящимся рядом 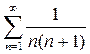(доказано ранее).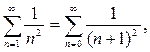

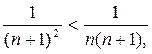
Значит, сходится.

Дата добавления: 2013-12-13