Лекция № 9 гармонические колебания

1. Гармоническое колебание

Колебательное движение – это повторяющиеся с течением времени движение, при котором, точка выйдя из положения равновесия перемещается в пространстве в некотором ограниченном интервале.

Колебания называются свободными, если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колеблющуюся точку.

Если при колебательном движении существует некоторое время, через которое место положения точки в пространстве повторяется, то такое колебание называется периодическим.

В природе и технике широко распространены периодические процес­сы. Вращение Земли вокруг своей оси и вокруг Солнца, работа сердца, ка­чание маятника, волны на воде, переменный электрический ток, свет, звук и т. д. являются примерами периодических процессов.

Из периодических движений наиболее простейшими являются гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Любое сложное колебание можно разложить в ряд гармонических колебаний.

или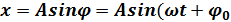

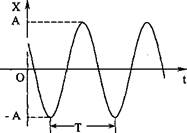
Гармонические колебания – это периодические колебания с периодом .

Х – смещение точки от положения равновесия, определяется синусом или косинусом.

А – амплитуда колебаний, максимальное отклонение от положения равновесия, которое достигается при колебательном движении.

– фаза колебаний. Фаза характеризует ту долю от амплитуды, которую будет иметь смещение в данный момент времени.

– начальная фаза характеризует ту долю от амплитуды, которую будет иметь смещение в начальный момент времени.

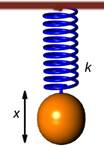Рассмотрим под действием каких сил совершаются колебания. Для этого необходимо знать m и х. Анализируя колебания грузика, мы видим, что грузик останавливается в крайних положениях, а затем движется в противопо­ложном направлении, т. е. грузик имеет переменные скорость и ускорение.

Скорость

Ускорение

Из второго закона Ньютона:

Под действием силы

груз совершает гармонические колебания.

m и ω –постоянные,

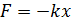
Гармонические колебания совершаются под действием упругих или квазиупругих сил.

Роль квазиупругой силы может выполнять результирующая сил:

(*)

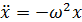или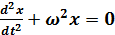

Уравнение (7) называется дифференциальным уравнением гармонического колебания.

2. Физический и математический маятник.

Рассмотрим физический маятник с углом отклонения φ. Физический маятник – это тело, имеющее ось вращения.

Для физического маятника необходимо использовать основное уравнение динамики

Если обозначить расстояние от центра вращения до точки приложения силы – а, плечо – р, то момент силы можно представить:

Знак минус показывает, что момент силы ведет к уменьшению угла поворота φ.

Так как угловая скорость

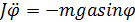
Если угол φ мал, то

(**)

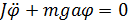
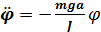Сравним (*) и (**)

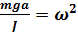
Период колебаний физического маятника

Период колебаний физического маятника зависит от распределения массы относительно оси вращения для малых углов отклонения.

Существует математический маятник – маятник, который имеет длину подвеса во много раз больше размеров самого маятника. Пусть а – длина математического маятника, тогда момент инерции математического маятника:

Период математического маятника:

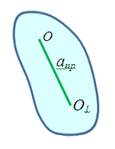
Движение математического маятника при больших углах отклонения будет периодическим, но не гармоническим (период колебаний будет зависеть от размаха). Гармоническими будут колебания при малых углах отклонения.

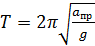
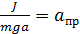
Приведенной длиной а_пр физического маятника называется такая длина математического маятника, при которой период физического маятника равен периоду математического маятника. Т_физ = Т_мат

Точка, удаленная от центра вращения на величину 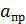называется центром качения. Ось качения и центр качения взаимообратимы.

3. Свободные электромагнитные колебания в колебательном контуре

В цепи, содержащей индуктивность и емкость, могут возникнуть электрические колебания, при которых электрические величины (заряды, токи, напряжения) периодически изменяются и которые сопровождаются взаимными превращениями энергии электрического и магнитного полей. Рассмотрим цепь, состоящую из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R (рис. 1). Такая цепь называется колебательным контуром. Колебания в контуре можно вызвать, сообщив обкладкам конденсатора некоторый начальный заряд ±q. Тогда в начальный момент времени при t = 0 между обкладками конденсатора возникает электрическое поле, энергия которого . Так как конденсатор замкнут на катушку индуктивности, то он начнет разряжаться, и в цепи потечет электрический ток I. В результате этого заряд на обкладках конденсатора (а значит, и энергия электрического поля) будет уменьшаться, а энергия магнитного поля катушки, которая равна 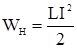, будет возрастать.

В том случае, когда сопротивление контура пренебрежимо мало (R» 0), потерями энергии в контуре на нагревание можно пренебречь, и, согласно закону сохранения энергии, полная энергия 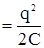+ = const. В контуре возникают электрические колебания, которые сопровождаются превращениями энергий электрического и магнитного полей.

Найдем уравнение колебаний в колебательном контуре. Согласно второму правилу Кирхгофа для этого контура (сумма падений напряжений на резисторе и конденсаторе равна ЭДС самоиндукции катушки):

IR + U_C = e_S,

где IR – напряжение на резисторе;

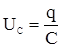напряжение на конденсаторе;

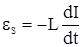– ЭДС самоиндукции, возникающая в катушке индуктивности. Следовательно,

. (***)

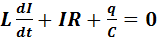Если ток считать положительным, когда конденсатор заряжается, тогда сила тока , ,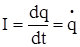

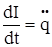и уравнение (***) примет вид .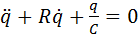

Разделив это уравнение на L, получим дифференциальное уравнение колебаний заряда q в контуре:

(****)

Дата добавления: 2013-12-13