Лекция № 10 Сложение гармонических колебаний

Свободные незатухающие колебания в контуре.

В этом случае сопротивление контура пренебрежимо мало (R» 0) и дифференциальное уравнение (****) имеет вид

.

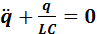Если ввести обозначение 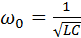, то это уравнение примет вид

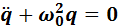(4)

Решением этого уравнения является функция

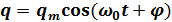(5)

Таким образом, заряд на обкладках конденсатора изменяется по гармоническому закону с частотой w₀. Эта частота называется собственной частотой контура.Период колебаний

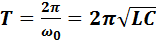. (6)

Эта формула называется формулой Томсона.

Напряжение на конденсаторе

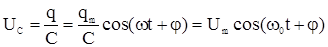, (7)

где 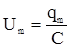– амплитуда напряжения.

Сравнивая формулы (7) и (5), мы видим, что колебания заряда и напряжения совпадают по фазе.

Сила тока в контуре

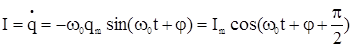, (8)

где I_m = 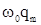– амплитуда силы тока.

Из выражений (8), (7) и (5) видно, что колебания тока опережают по фазе колебания заряда и напряжения на 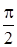, т.е., когда ток достигает максимального значения, заряд (и напряжение) обращаются в нуль, и наоборот.

1. Сложение колебаний одинакового направления с одинаковыми частотами

Сложение колебаний мы наблюдаем довольно часто. Например, при интерференции света, звука и т. д. Очень просто осуществить сложение механических колебаний, если, например, в случае пружинного маятника будет колебаться и точка крепления пружины. Например, пружинный ма­ятник подвешен к потолку вагона движущегося поезда. Тогда собственные колебания грузика на пружине будут складываться с вертикальными коле­баниями вагона.

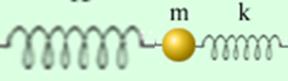Рассмотрим случай, когда складываются колебания направленные вдоль одной прямой и с одинаковой частотой.

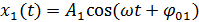
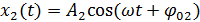
Тогда результирующее колебание грузика будет равно:

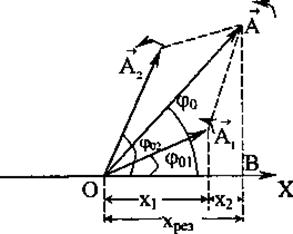
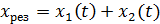
Чтобы осуществить сложение, применим метод векторных диаграмм, в котором гармоническое колебание может быть представлено с помощью вектора амплитуды, вращающегося против часовой стрелки с угловой ско­ростью со вокруг оси О, перпендику­лярный плоскости чертежа (рис. 1). Действительно, в начальный момент

при t = 0 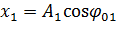и

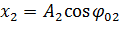
Отложим вектор 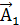под углом φ₀₁ к оси ОХ (рис) и вектор 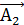под углом φ_02. Тогда для амплитуды А ре­зультирующего колебания, применяя теорему косинусов, получаем

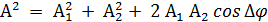, где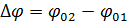

Отсюда получаем

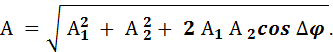(1)

Как видно из рис., тангенс начальной фазы φ₀ результирующего колебания

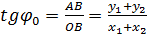
где x₁, х₂ - проекции векторов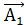и 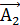на ось ОХ, а у₁ и у₂ на ось OY (на рис. не показаны)

АВ ₌ y₁ +y₂ ОВ = х₁+х₂

Получаем окончательно

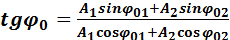(2)

Итак, результирующее колебание будет гармоническим тоже с часто­той ω, поскольку векторы 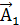и 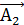вращаются с одной и той же угловой скоростью ω, т. е. грузик теперь будет смещаться по закону

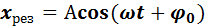
где А и φ_о определяются соответственно выражениями (1) и (2).

Рассмотрим частные случаи сложения колебаний:

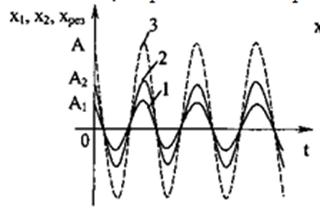а ) синфазных 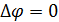, т.е. .

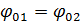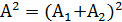или

Дата добавления: 2013-12-13