При сложении одинаково направленных противофаз­ных колебаний наблюдается ослабление колебаний

При сложении одинаково направленных синфазных колебаний происходит усиление колебаний

б) противофазных

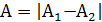
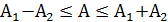
2. Сложение гармонических колебаний одинакового направления мало отличаются по частоте. Биения.

Особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. Результирующее движение можно рассматривать как колебание с пульсирующей амплитудой. Действительно, пусть одно колебание

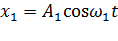а второе

причем . Пусть , тогда . Малое отличие по частоте означает, что 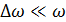. При­мем для простоты, что a₁ = А₂ = А.

Результирующее смещение будет равно:

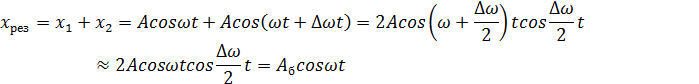
Здесь мы пренебрегли в силу малости членом по сравнению с ω.

Мы получили уравнение биений:

Где – амплитуда биений:

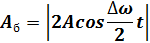
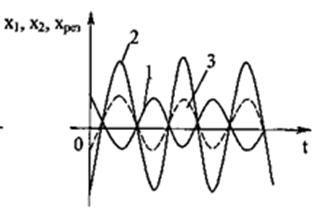
Построим график биений, т. е. x_pe3(t):

Из графика видно, что биения представляют собой негармонические колебания, т. к. в этих колебаниях амплитуда не постоянна, а пульсирует

от 2А до нуля, при этом период биений равен .

Биения используют в металлоискателях. Когда внешний электриче­ский контур металлоискателя будет находиться над металлом, его частота уменьшается по сравнению с таким же внутренним его контуром на вели­чину . В результате возникают биения, которые прослушиваются с по­мощью наушников.

3. Сложение взаимно перпендикулярных колебаний с одинаковыми частотами.

Перейдем к сложению двух взаимно перпендикулярных гар­монических колебаний точки, совершающихся вдоль координатных осей ОХ и OY с одной и той же частотой .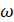

Примером может служить математический маятник с двумя степеня­ми свободы, т. е. маятник, который одновременно колеблется в двух вза­имно перпендикулярных направлениях. Это можно сделать, если грузику, колеблющемуся в одной плоскости, дать толчок в перпендикулярном на­правлении.

Запишем уравнения колебаний по двум осям:

t,

,

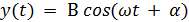где α - разность фаз этих колебаний.

Уравнение траектории результирующего движения грузика (точки) в плоскости XOY можно получить, исключив из выражений для х и у пара­метр t.

Выразим из первого уравнения и подставим это выражение в преобразованное второе:

и окончательно

(3)

Исключив из уравнений колебаний время t, мы получили траекторию результирующего движения точ­ки. Траектория имеет форму эллипса (3), причем точка опи­сывает этот эллипс (рис.) за время, равное периоду складываемых колебаний: .

Рассмотрим частные слу­чаи сложения взаимно перпен­дикулярных колебаний.

α = 0, 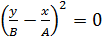, эллипс вырождается в отрезок прямой Колебание точки про­исходит вдоль прямой с амплитудой
, т. е. колебание точки происходит вдоль прямой во 2-й и 4-й четвертях
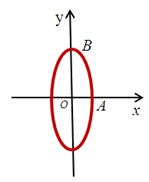
, Точка описывает эллипс причем при точка движется по часовой стрелке, а при против часовой стрел­ки.
, А=В получаем движение точки по окружности, т. е. эллипс вырождается в окружность

4. Сложение взаимно перпендикулярных колебаний с разными частота­ми. Фигуры Лиссажу.

Рассмотрим сложение гармонических взаимно пер­пендикулярных колебаний с частотами ω₁ и ω₂.

где (р и q - целые числа).

Удобно наблюдать траекторию результирующего движения точки на экра­не осциллографа, когда на горизонтально отклоняющиеся пластины пода­ется переменное напряжение с частотой ω₁, а на вертикально отклоняю­щиеся - с частотой ω₂. Значения координат х и у колеблющейся точки од­новременно повторяются через одинаковые промежутки времени То, равные общему наименьшему кратному: 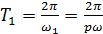и 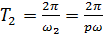периодов колебаний вдоль осей ОХ и OY. Поэтому траектория точки - замкну­тая кривая, форма которой зависит от соотношения амплитуд, частот и на­чальных фаз складываемых колебаний.

Такие замкнутые траектории точки, одновременно совершающей гар­монические колебания в двух взаимно перпендикулярных направлениях, называются фигурами Лиссажу. Фигуры Лиссажу вписываются в прямо­угольник, центр которого совпадает с началом координат, а стороны параллельны осям координат ОХ и OY и расположены по обе стороны от них на расстояниях, соответственно равных А и В. Отношение частот рω и qω равно отношению числа касаний соответствующей им фигуры Лиссажу со стороной прямоугольника, параллельной оси OY, и со стороной, парал­лельной оси ОХ.

Пусть, например, имеем два колебания с частотами, отличающимися в два раза:

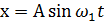
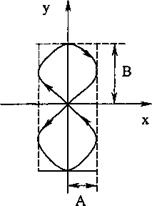
Где . Получим траекторию в виде «восьмерки», вписанной в прямоугольник

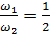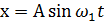Если , a и

то получим траекторию, представленную

На рис. показаны простые фигуры Лиссажу. Чем ближе к единице рациональная дробь, выражающая отношение частот колебаний , тем сложнее оказывается фигура Лиссажу.

Французский математик Фурье устано­вил следующую теорему для пе­риодических колебаний: Любое периодическое негар­моническое колебание с частотой со всегда можно представить в виде суммы гармонических колебаний. Таким образом, периодическое колеба­ние U(t) можно представить в виде

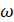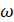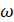. Частота называется основной частотой; частоты 2, З, 4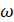... - это обертоны или гармоники. Говорят, например, вторая гармоника имеет ам­плитуду А₂, третья А_з и т. д.

Дата добавления: 2013-12-13