Уравнение затухающих колебаний

СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

Свободные затухающие колебания — колебания, амплитуды которых из-за потерь энергии с течением времени уменьшаются. Простейшим механизмом уменьшения энергии колебаний является ее превращение в теплоту вследствие трения в механических колебательных системах.

Рассмотрим колебания пружинного маятника, помещенного в вязкую среду. Колебания будут затухающими, и при колебаниях, если скорость грузика массы m будет мала, можно считать, что сила сопротивления пропорциональна скорости движения, т. е. F_сопр = – r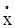, где r – коэффициент сопротивления, зависящий от вязкости среды. Т.о. на маятник действуют силы упругости и сопротивления, по 2 закону Ньютона:

m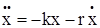

или 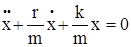, окончательно получим

, (*)

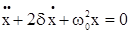где 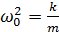; 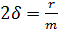. Здесь d – коэффициент, характеризующий быстроту затухания, он называется коэффициентом затухания, он пропорционален коэффициенту сопротивления r; «двойка» введена для удобства вычислений в дальнейшем.

Уравнение (*) называется дифференциальным уравнением затухающих колебаний. Решение такого уравнения:

х(t) = А₀ е^–dt cos(wt + j₀), (**)

где А₀ и j₀ – постоянные, зависящие от начальных условий, т. е. при t = 0, а частота колебаний

,

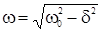При малом сопротивлении, когда d мало, 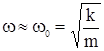, т. е. частота равна частоте собственных незатухающих колебаний. При большом же затухании, когда 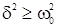, получаем нулевую или мнимую частоту, т. е. колебание отсутствует, мы имеем так называемый «апериодический процесс».

График затухающего колебания. Штриховая кривая показывает уменьшение амплитуды по закону экспоненты.

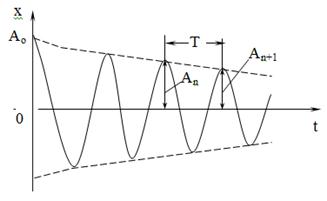
При большом затухании получаем апериодический процесс, т. е. система не совершает даже одного полного колебания.

Дата добавления: 2013-12-13